ж–җжіўйӮЈеҘ‘ж•°еҲ—
0гҖҒ1гҖҒ1гҖҒ2гҖҒ3гҖҒ5гҖҒ8гҖҒ13гҖҒ21гҖҒ34гҖҒ...
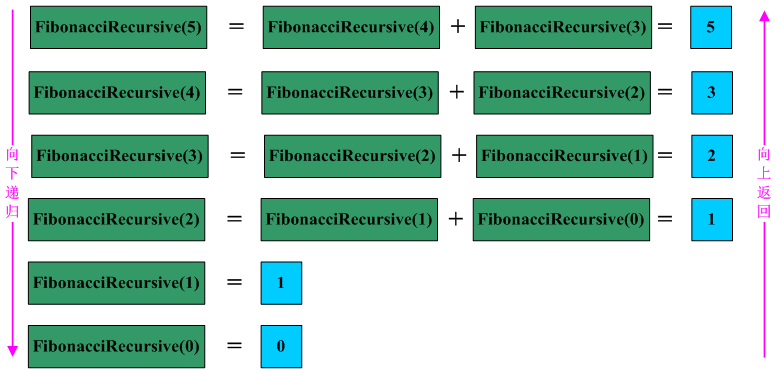
дёҖгҖҒйҖ’еҪ’ж–№ејҸпјҡF(0)=0пјҢF(1)=1пјҢF(n)=F(n-1)+F(n-2)пјҲnвүҘ2пјҢnвҲҲN*пјү
з”ЁйҖ’еҪ’йңҖиҰҒжіЁж„Ҹд»ҘдёӢдёӨзӮ№пјҡ(1) йҖ’еҪ’е°ұжҳҜеңЁиҝҮзЁӢжҲ–еҮҪж•°йҮҢи°ғз”ЁиҮӘиә«гҖӮ(2) еңЁдҪҝз”ЁйҖ’еҪ’зӯ–з•Ҙж—¶пјҢеҝ…йЎ»жңүдёҖдёӘжҳҺзЎ®зҡ„йҖ’еҪ’з»“жқҹжқЎд»¶пјҢз§°дёәйҖ’еҪ’еҮәеҸЈгҖӮ
|
1 2 3 4 5 6 7 8 9 10 11 |
int Fibonacci1(int index){ if(index<=0){ return 0; } else if(index==1){ return 1; } else{ return Fibonacci1(index-1)+Fibonacci1(index-2); } } |
еҲҶжһҗдёҠејҸпјҢеңЁи®Ўз®—F(n)ж—¶пјҢйңҖиҰҒи®Ўз®—F(2)еҲ°F(n-1)жҜҸдёҖйЎ№зҡ„еҖјпјҢжҳҫ然еӯҳеңЁзқҖеҫҲеӨҡйҮҚеӨҚи®Ўз®—гҖӮеҰӮдҪ•еҮҸе°‘йҮҚеӨҚи®Ўз®—пјҢеҸҜд»Ҙз”ЁдёҖдёӘж•°з»„еӯҳеӮЁжүҖжңүе·Із»Ҹи®Ўз®—иҝҮзҡ„йЎ№пјҢз”Ёз©әй—ҙжҚўеҸ–ж—¶й—ҙгҖӮж—¶й—ҙеӨҚжқӮеәҰдёә пјҢз©әй—ҙеӨҚжқӮеәҰд№ҹдёә
пјҢз©әй—ҙеӨҚжқӮеәҰд№ҹдёә гҖӮ
гҖӮ
е°ҫйҖ’еҪ’ж–№ејҸпјҡ
еҮҪж•°и°ғз”ЁеҮәзҺ°еңЁи°ғз”ЁиҖ…еҮҪж•°зҡ„е°ҫйғЁ, еӣ дёәжҳҜе°ҫйғЁ, жүҖд»Ҙж №жң¬жІЎжңүеҝ…иҰҒеҺ»дҝқеӯҳд»»дҪ•еұҖйғЁеҸҳйҮҸ. зӣҙжҺҘи®©иў«и°ғз”Ёзҡ„еҮҪж•°иҝ”еӣһж—¶и¶ҠиҝҮи°ғз”ЁиҖ…, иҝ”еӣһеҲ°и°ғз”ЁиҖ…зҡ„и°ғз”ЁиҖ…еҺ»гҖӮе°ҫйҖ’еҪ’е°ұжҳҜжҠҠеҪ“еүҚзҡ„иҝҗз®—з»“жһңпјҲжҲ–и·Ҝеҫ„пјүж”ҫеңЁеҸӮж•°йҮҢдј з»ҷдёӢеұӮеҮҪж•°пјҢж·ұеұӮеҮҪж•°жүҖйқўеҜ№зҡ„дёҚжҳҜи¶ҠжқҘи¶Ҡз®ҖеҚ•зҡ„й—®йўҳпјҢиҖҢжҳҜи¶ҠжқҘи¶ҠеӨҚжқӮзҡ„й—®йўҳпјҢеӣ дёәеҸӮж•°йҮҢеёҰжңүеүҚйқўиӢҘе№ІжӯҘзҡ„иҝҗз®—и·Ҝеҫ„гҖӮеҜ№дәҺйҳ¶д№ҳиҖҢиЁҖпјҢи¶Ҡж·ұ并дёҚж„Ҹе‘ізқҖи¶ҠеӨҚжқӮгҖӮ
е°ҫйҖ’еҪ’жҳҜжһҒе…¶йҮҚиҰҒзҡ„пјҢдёҚз”Ёе°ҫйҖ’еҪ’пјҢеҮҪж•°зҡ„е Ҷж ҲиҖ—з”Ёйҡҫд»Ҙдј°йҮҸпјҢйңҖиҰҒдҝқеӯҳеҫҲеӨҡдёӯй—ҙеҮҪж•°зҡ„е Ҷж ҲгҖӮжҜ”еҰӮf(n,В sum)В =В f(n-1)В +В value(n)В +В sum;В дјҡдҝқеӯҳnдёӘеҮҪж•°и°ғз”Ёе Ҷж ҲпјҢиҖҢдҪҝз”Ёе°ҫйҖ’еҪ’f(n,В sum)В =В f(n-1,В sum+value(n));В иҝҷж ·еҲҷеҸӘдҝқз•ҷеҗҺдёҖдёӘеҮҪж•°е Ҷж ҲеҚіеҸҜпјҢд№ӢеүҚзҡ„еҸҜдјҳеҢ–еҲ еҺ»гҖӮ
|
1 2 3 4 5 6 7 8 |
int FibonacciTailRecursive(int index,int ret1,int ret2){ if(index==0) return ret1; else if(index==1){ return ret2; } return FibonacciTailRecursive(index-1,ret2,ret1+ret2); } |
дәҢгҖҒж•°з»„е®һзҺ° В В з©әй—ҙеӨҚжқӮеәҰе’Ңж—¶й—ҙеӨҚжқӮеәҰйғҪжҳҜ0(n)пјҢж•ҲзҺҮдёҖиҲ¬пјҢжҜ”йҖ’еҪ’жқҘеҫ—еҝ«гҖӮ
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
int Fibonacci2(int index){ if(index<=0){ return 0; } else if(index==1){ return 1; } int *a=new int[index]; a[0]=a[1]=1; for(int i=2;i<index;i++){ a[i]=a[i-1]+a[i-2]; } int m=a[index-1]; delete a; return m; } |
дёүгҖҒжұӮи§ЈйҖҡйЎ№е…¬ејҸ
F(n)=F(n-1)+F(n-2)еҸҜд»Ҙеҫ—еҲ°F(n)зҡ„зү№еҫҒж–№зЁӢдёә гҖӮеҫ—еҲ°
гҖӮеҫ—еҲ°
жүҖд»ҘеӯҳеңЁ дҪҝеҫ—пјҡ
дҪҝеҫ—пјҡ
д»Је…Ҙ пјҢи§Јеҫ—
пјҢи§Јеҫ— пјҢеҚі
пјҢеҚі

|
1 2 3 4 5 6 |
#include <cmath> using namespace std; int Fibonacci3(int n){ double sqrt5=sqrt((double)5); return (pow((1+sqrt5),n)-pow((1-sqrt5),n))/(pow((double)2,n)*sqrt5); } |
з”ұдәҺdoubleзұ»еһӢзҡ„зІҫеәҰиҝҳдёҚеӨҹпјҢжүҖд»ҘзЁӢеәҸз®—еҮәжқҘзҡ„з»“жһңдјҡжңүиҜҜе·®пјҢеҰӮжһңжҠҠе…¬ејҸеұ•ејҖи®Ўз®—пјҢеҫ—еҮәзҡ„з»“жһңе°ұжҳҜжӯЈзЎ®зҡ„гҖӮ
|
1 2 3 4 5 6 7 8 9 10 11 |
//дәҢеҲҶжі•и®Ўз®—aзҡ„nж¬Ўж–№еҮҪж•° int pow(int a,int n){ int ans=1; while(n){ if(n&1) ans*=a; a*=a; n>>=1; } return ans; } |
еӣӣгҖҒqueue<int>е®һзҺ°
ж—¶й—ҙеӨҚжқӮеәҰжҳҜ0(n)пјҢз©әй—ҙеӨҚжқӮеәҰжҳҜ0(1)
f(n)=f(n-1)+f(n-2)пјҢf(n)еҸӘе’Ңf(n-1)е’Ңf(n-2)жңүе…іпјҢf(n)е…ҘйҳҹеҲ—еҗҺпјҢf(n-2)е°ұеҸҜд»ҘеҮәйҳҹеҲ—дәҶгҖӮ
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
#include <queue> int Fibonacci4(int index){ if(index<=0){ return 0; } else if(index==1){ return 1; } queue<int> myqueue; myqueue.push(1); myqueue.push(1); for(int i=2;i<index;i++){ myqueue.push(myqueue.front()+myqueue.back()); myqueue.pop();//дҝқиҜҒйҳҹеҲ—дёӯе§Ӣз»ҲеҸӘжңүдёӨдёӘеҖј } return myqueue.back(); } |
В queueзҡ„back()е’Ңfront()еҖјеҫ—з ”з©¶гҖӮ
дә”гҖҒиҝӯд»Је®һзҺ°
иҝӯд»Је®һзҺ°жҳҜжңҖй«ҳж•Ҳзҡ„пјҢж—¶й—ҙеӨҚжқӮеәҰжҳҜ0(n)пјҢз©әй—ҙеӨҚжқӮеәҰжҳҜ0(1)гҖӮ
дёҖгҖҒзЎ®е®ҡиҝӯд»ЈеҸҳйҮҸгҖӮеңЁеҸҜд»Ҙз”Ёиҝӯд»Јз®—жі•и§ЈеҶізҡ„й—®йўҳдёӯпјҢиҮіе°‘еӯҳеңЁдёҖдёӘзӣҙжҺҘжҲ–й—ҙжҺҘең°дёҚж–ӯз”ұж—§еҖјйҖ’жҺЁеҮәж–°еҖјзҡ„еҸҳйҮҸпјҢиҝҷдёӘеҸҳйҮҸе°ұжҳҜиҝӯд»ЈеҸҳйҮҸгҖӮ
дәҢгҖҒе»әз«Ӣиҝӯд»Је…ізі»ејҸгҖӮжүҖи°“иҝӯд»Је…ізі»ејҸпјҢжҢҮеҰӮдҪ•д»ҺеҸҳйҮҸзҡ„еүҚдёҖдёӘеҖјжҺЁеҮәе…¶дёӢдёҖдёӘеҖјзҡ„е…¬ејҸпјҲжҲ–е…ізі»пјүгҖӮиҝӯд»Је…ізі»ејҸзҡ„е»әз«ӢжҳҜи§ЈеҶіиҝӯд»Јй—®йўҳзҡ„е…ій”®пјҢйҖҡеёёеҸҜд»ҘдҪҝз”ЁйҖ’жҺЁжҲ–еҖ’жҺЁзҡ„ж–№жі•жқҘе®ҢжҲҗгҖӮ
дёүгҖҒеҜ№иҝӯд»ЈиҝҮзЁӢиҝӣиЎҢжҺ§еҲ¶гҖӮеңЁд»Җд№Ҳж—¶еҖҷз»“жқҹиҝӯд»ЈиҝҮзЁӢпјҹиҝҷжҳҜзј–еҶҷиҝӯд»ЈзЁӢеәҸеҝ…йЎ»иҖғиҷ‘зҡ„й—®йўҳгҖӮдёҚиғҪи®©иҝӯд»ЈиҝҮзЁӢж— дј‘жӯўең°йҮҚеӨҚжү§иЎҢдёӢеҺ»гҖӮиҝӯд»ЈиҝҮзЁӢзҡ„жҺ§еҲ¶йҖҡеёёеҸҜеҲҶдёәдёӨз§Қжғ…еҶөпјҡдёҖз§ҚжҳҜжүҖйңҖзҡ„иҝӯд»Јж¬Ўж•°жҳҜдёӘзЎ®е®ҡзҡ„еҖјпјҢеҸҜд»Ҙи®Ўз®—еҮәжқҘпјӣеҸҰдёҖз§ҚжҳҜжүҖйңҖзҡ„иҝӯд»Јж¬Ўж•°ж— жі•зЎ®е®ҡгҖӮеҜ№дәҺеүҚдёҖз§Қжғ…еҶөпјҢеҸҜд»Ҙжһ„е»әдёҖдёӘеӣәе®ҡж¬Ўж•°зҡ„еҫӘзҺҜжқҘе®һзҺ°еҜ№иҝӯд»ЈиҝҮзЁӢзҡ„жҺ§еҲ¶пјӣеҜ№дәҺеҗҺдёҖз§Қжғ…еҶөпјҢйңҖиҰҒиҝӣдёҖжӯҘеҲҶжһҗеҮәз”ЁжқҘз»“жқҹиҝӯд»ЈиҝҮзЁӢзҡ„жқЎд»¶гҖӮ
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
int Fibonacci5(int index){ int i,a=1,b=1,c=1; if(index<=0){ return 0; } else if(index==1){ return 1; } for(int i=2;i<index;i++){ c=a+b;//иҫ—иҪ¬зӣёеҠ жі•пјҲзұ»дјјдәҺжұӮжңҖеӨ§е…¬зәҰж•°зҡ„иҫ—иҪ¬зӣёйҷӨжі•пјү a=b; b=c; } return c; } |
е…ӯгҖҒеҲҶжІ»зӯ–з•Ҙ
жіЁж„ҸеҲ°Fibonacciж•°еҲ—жҳҜдәҢйҳ¶йҖ’жҺЁж•°еҲ—пјҢжүҖд»Ҙи®ҜеңЁдёҖдёӘ2*2зҡ„зҹ©йҳөпјҢдҪҝеҫ—
еҰӮдҪ•жұӮи§ЈAзҡ„ж–№е№Ӯпјҹ гҖӮжңҖзӣҙжҺҘзҡ„ж–№жі•е°ұжҳҜйҖҡиҝҮ
гҖӮжңҖзӣҙжҺҘзҡ„ж–№жі•е°ұжҳҜйҖҡиҝҮ ж¬Ўд№ҳжі•гҖӮдҪҶеҪ“nеҫҲеӨ§ж—¶пјҢжҜ”еҰӮ10000000000пјҢжҳҫз„¶ж— жі•и®Ўз®—гҖӮ
ж¬Ўд№ҳжі•гҖӮдҪҶеҪ“nеҫҲеӨ§ж—¶пјҢжҜ”еҰӮ10000000000пјҢжҳҫз„¶ж— жі•и®Ўз®—гҖӮ


з”ЁдәҢиҝӣеҲ¶иЎЁзӨәnпјҡ пјҢе…¶дёӯ
пјҢе…¶дёӯ

еҰӮжһңиғҪеӨҹеҫ—еҲ° зҡ„еҖјпјҢе°ұеҸҜд»ҘйҖҡиҝҮ
зҡ„еҖјпјҢе°ұеҸҜд»ҘйҖҡиҝҮ ж¬Ўд№ҳжі•еҫ—еҲ°
ж¬Ўд№ҳжі•еҫ—еҲ° гҖӮ
гҖӮ
йҖ’еҪ’еҸҜеҫ—
д»Јз Ғжңүй—®йўҳ
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
void multiply(int c[2][2],int a[2][2],int b[2][2],int mod) { int tmp[4]; tmp[0]=a[0][0]*b[0][0]+a[0][1]*b[1][0]; tmp[1]=a[0][0]*b[0][1]+a[0][1]*b[1][1]; tmp[2]=a[1][0]*b[0][0]+a[1][1]*b[1][0]; tmp[3]=a[1][0]*b[0][1]+a[1][1]*b[1][1]; c[0][0]=tmp[0]%mod; c[0][1]=tmp[1]%mod; c[1][0]=tmp[2]%mod; c[1][1]=tmp[3]%mod; }//и®Ўз®—зҹ©йҳөд№ҳжі•пјҢc=a*b int Fibonacci6(int n,int mod)//modиЎЁзӨәж•°еӯ—еӨӘеӨ§ж—¶йңҖиҰҒжЁЎзҡ„ж•° { if(n==0)return 0; else if(n<=2)return 1;//иҝҷйҮҢиЎЁзӨә第0йЎ№дёә0пјҢ第1пјҢ2йЎ№дёә1 int a[2][2]={{1,1},{1,0}}; int result[2][2]={{1,0},{0,1}};//еҲқе§ӢеҢ–дёәеҚ•дҪҚзҹ©йҳө int s; n-=2; while(n>0) { if(n%2 == 1) multiply(result,result,a,mod); multiply(a,a,a,mod); n /= 2; }//дәҢеҲҶжі•жұӮзҹ©йҳөе№Ӯ s=(result[0][0]+result[0][1])%mod;//з»“жһң return s; } |
еҸӮиҖғпјҡhttp://www.jb51.net/article/37286.htm
дјҳе…ҲйҳҹеҲ—дёүеӨ§еҲ©еҷЁвҖ”вҖ”дәҢйЎ№е ҶгҖҒж–җжіўйӮЈеҘ‘е ҶгҖҒPairing е Ҷ
http://dsqiu.iteye.com/blog/1714961


и®Іеҫ—еҘҪиөһ ж„ҹи°ўпјҒ