机器学习领域,学习问题实际情况往往是非线性的,所谓的线性较少存在。但是由于线性方法的大量存在,那么就不可避免的涉及到一个问题,如何将这些线性的学习方法应用在非线性问题上或者说获得非线性识别能力?
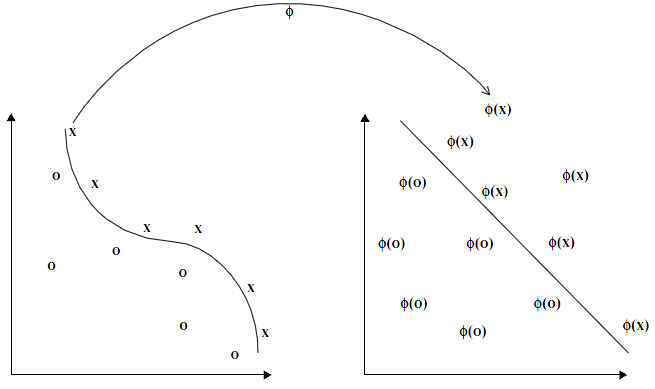
Fig.1 映射函数  将数据映射到一个高维空间中,使得非线性的模式线性可分。核方法计算输入向量与训练样本间的内积表示数据点之间的相似程度。
将数据映射到一个高维空间中,使得非线性的模式线性可分。核方法计算输入向量与训练样本间的内积表示数据点之间的相似程度。
考虑嵌入映射(embedding map): 映射到高维空间,这个空间可以是有限维空间,也可以是无穷维空间。它是一个Hilbert空间。任何核方法包括:1)映射方法(embed the data into a space where the patterns can be discovered as linear relations) 2)学习算法来发掘映射空间中的线性模式 (Represent linear patterns efficiently in high-dimensional space to ensure adequate representational power)
映射到高维空间,这个空间可以是有限维空间,也可以是无穷维空间。它是一个Hilbert空间。任何核方法包括:1)映射方法(embed the data into a space where the patterns can be discovered as linear relations) 2)学习算法来发掘映射空间中的线性模式 (Represent linear patterns efficiently in high-dimensional space to ensure adequate representational power)
实际上,svm核方法升维,使得在高维上的线性切割,投射到实际空间就变为非线性的切割;lr通过增加大量非线性特征,使得获得非线性切割能力;深度学习通过二层以上神经网络获得非线性切割。核心都需要有非线性识别能力。
Least Squares Linear Regression
首先让我们抛开所谓的核方法,而从least squares linear regression(最小二乘线性回归)这个通俗易懂的问题切入。
给定训练集 ,
,
 维输入向量
维输入向量 ,需要找出一个决策函数,推断输入
,需要找出一个决策函数,推断输入 相对应的输出值
相对应的输出值 。最简单的方法就是通过一个线性函数
。最简单的方法就是通过一个线性函数 将
将 映射到
映射到 。
。
 ,要求
,要求
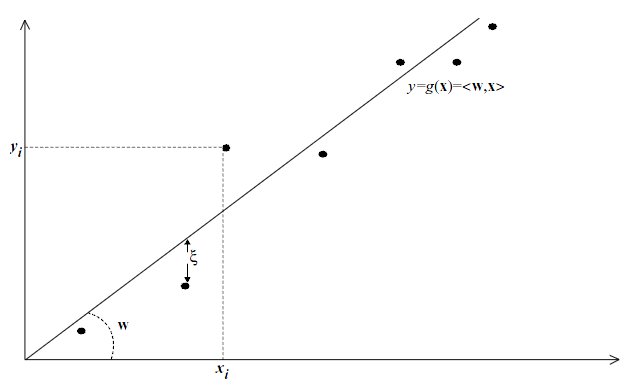
Fig.2. A one-dimensional  =1 linear regression problem.
=1 linear regression problem.
![X_{l\times n}w_{n\times 1}=y_{l\times 1},X=[x{_1}^{'};...;x{_l}^{'}],y=(y_1,...,y_{l})^{'}](http://ramsey16.net/wp-content/plugins/latex/cache/tex_3a10a01b4c227f1febc7d23effc465e5.gif)
当存储数据的矩阵 的行维数(即数据点的个数)小于数据点的维数时,
的行维数(即数据点的个数)小于数据点的维数时, 有无穷多个解(describe the data exactly),此时选择的标准是取最小范数的
有无穷多个解(describe the data exactly),此时选择的标准是取最小范数的 。当
。当 的行维数大于列维数时,且数据点存在噪声,此时不存在准确的模式(exact pattern),此时应使误差最小。一般情况下处理有噪声的小数据集,我们应选择
的行维数大于列维数时,且数据点存在噪声,此时不存在准确的模式(exact pattern),此时应使误差最小。一般情况下处理有噪声的小数据集,我们应选择 ,使误差最小及其范数最小。
,使误差最小及其范数最小。
 为误差,
为误差, ,寻找一个映射函数使得训练误差最小。通常选择误差的平方和
,寻找一个映射函数使得训练误差最小。通常选择误差的平方和 ,寻找
,寻找 使得训练误差总和(collective loss)最小。
使得训练误差总和(collective loss)最小。
令 ,损失函数
,损失函数 ,求取损失函数对参数
,求取损失函数对参数 的偏导并使其为0向量。
的偏导并使其为0向量。
 从而有
从而有 (normal equations)(1)
(normal equations)(1)
当 的逆存在时,该最小二乘问题的解为:
的逆存在时,该最小二乘问题的解为:
 为
为 的矩阵,解一个
的矩阵,解一个 的线性方程组时间复杂度为
的线性方程组时间复杂度为 。对于新的输入测试数据点,其预测输出为
。对于新的输入测试数据点,其预测输出为 。
。
Remark1: 对偶表达形式
如果 的逆存在,
的逆存在, 可以表示为训练数据点的线性组合,如下所示
可以表示为训练数据点的线性组合,如下所示

Remark2: 伪逆(Pseudo-inverse)
如果 奇异(singular),则寻找满足式1)的最小范数的
奇异(singular),则寻找满足式1)的最小范数的 。并在范数值大小与损失函数间进行trade-off,这个方法称为岭回归(Ridge Regression)。
。并在范数值大小与损失函数间进行trade-off,这个方法称为岭回归(Ridge Regression)。
Ridge Regression
Definition:
 为正数,通过控制
为正数,通过控制 的大小调整范数大小与损失函数间的tradeoff。
的大小调整范数大小与损失函数间的tradeoff。
Primal Solution:(原始解)
同样对代价函数求取参数向量 的偏导并使其为0,可以得到
的偏导并使其为0,可以得到

 为
为 的单位阵
的单位阵
显然 可逆当
可逆当 ,该方程解为
,该方程解为

解这个有个 未知数,
未知数, 个等式的线性方程组时间复杂度为
个等式的线性方程组时间复杂度为 。
。

 需要
需要 次相乘,复杂度为
次相乘,复杂度为
Dual Solution:(对偶解)
 where
where 




where  ,
,
解这个有 未知数,
未知数, 个等式的线性方程组时间复杂度为
个等式的线性方程组时间复杂度为 。
。

where  ,
, 需要次
需要次 相乘,复杂度为
相乘,复杂度为 。(more costly)
。(more costly)
所以!!包含在训练样本中的信息可以通过训练样本对的内积获得。 ,
, 。
。
当输入一个新的样本 ,预测函数所需要的信息正是训练样本与
,预测函数所需要的信息正是训练样本与 的内积。
的内积。
 矩阵称为Gram matrix,
矩阵称为Gram matrix, 。显然当训练样本的特征维数
。显然当训练样本的特征维数 大于训练样本数
大于训练样本数 时,对偶解法更为高效。
时,对偶解法更为高效。
结论:岭回归算法只需要求解数据点之间的内积就可以求解。It’s amazing!