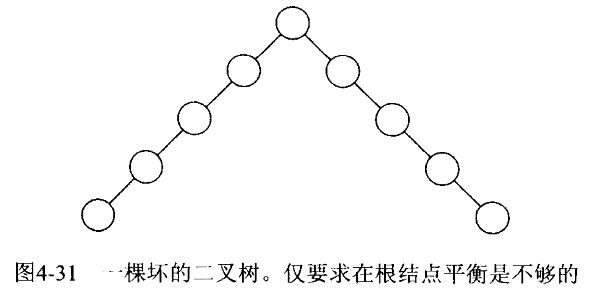
AVL树是带有平衡条件的二叉查找树。
想法1、要求左右子树具有相同的高度。这种想法并不强求树的深度要浅。
想法2、要求每个结点都必须有相同高度的左子树和右子树。如果空子树的高度定义为-1,那么只具有 个结点的理想平衡二叉树满足这个条件。
个结点的理想平衡二叉树满足这个条件。
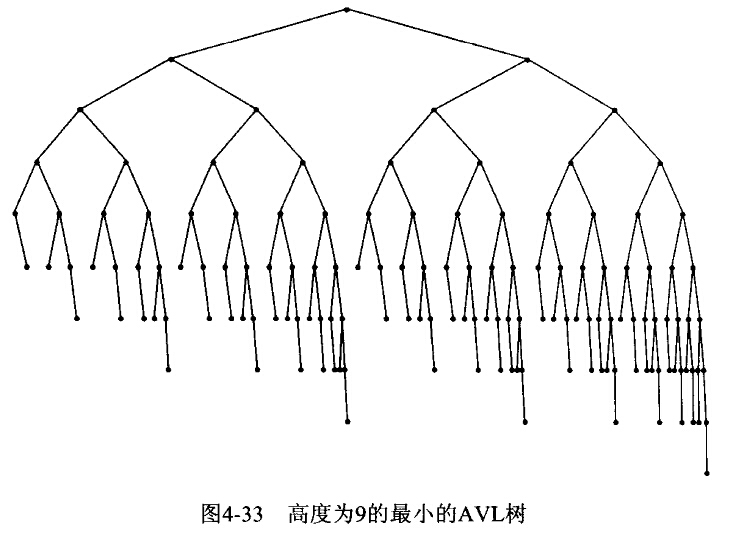
一棵AVL树是其每个结点的左子树和右子树的高度最多差1的二叉查找树。每个结点(会在其结点结构中)保留高度信息。如图是一棵具有最少结点(143)高度为9的AVL树。这棵树的左子树是高度为7且结点数最少的AVL树,右子树是高度为8且结点数最少的AVL树。
结论:在高度为h的AVL树中,最少结点数S(h)由 给出。对于
给出。对于
 与斐波那契数列密切相关。由此可以推出关于AVL树的高度的界。
与斐波那契数列密切相关。由此可以推出关于AVL树的高度的界。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
class AVLTree{ public: AVLTree(){root=NULL;} //public版本的重载供用户使用 void insert(const int&x){AvlTree_Insert(x,root);} void remove(const int&x){AvlTree_Remove(x,root);} private: struct AvlNode{ int element; AvlNode *left; AvlNode *right; int height; AvlNode( const int & theElement, AvlNode *lt, AvlNode *rt, int h = 0 ) : element( theElement ), left( lt ), right( rt ), height( h ) { } }; AvlNode *root; void AvlTree_Insert(const int &x,AvlNode * &t); void AvlTree_Remove(const int &x,AvlNode * &t); void leftChildSingleRotation(AvlNode * &t); void rightChildSingleRotation(AvlNode * &t); void leftChildDoubleRotation(AvlNode * &t); void rightChildDoubleRotation(AvlNode * &t); //结点的高度,空结点的高度为-1 int height(AvlNode * &t){ return t==NULL?-1:t->height;} int max(int a,int b){return a<b?b:a;} int powerof2(int x){ if(x==0)return 1; int m=1; while(--x>=0) m*=2; return m; } //max和min使用递归的话不能使用引用形参,不能返回引用 AvlNode *max_node(AvlNode *root){ if(!root) return NULL; if(root->right) return max_node(root->right); else return root; } AvlNode *min_node(AvlNode*root){ if(root) while(root->left) root=root->left; return root; } }; |
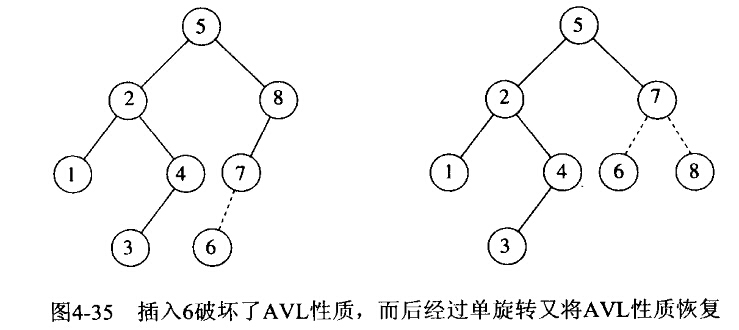
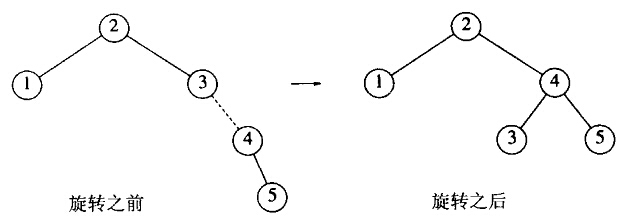
将6插入到AVL树中会破坏项为8的结点的平衡条件。通过对树进行简单的修正来做到,称为旋转。
将必须重新平衡的结点称为 。由于任意结点最多有两个子结点,因此高度不平衡时,
。由于任意结点最多有两个子结点,因此高度不平衡时, 点的两棵子树的高度差为2。这种不平衡可能出现在以下4种情况:
点的两棵子树的高度差为2。这种不平衡可能出现在以下4种情况:
其实我们可以把(1)、(4)看做一种情况,即插入发生在“外边”。(2)、(4)看做一种情况,即插入发生在“内部”。
对于第一种情况通过对树的单旋转完成调整,对于第二种情况通过对树的双旋转完成调整。
单旋转
|
1 2 3 4 5 6 7 8 9 |
//左单旋转,LL类型 void AVLTree::leftChildSingleRotation(AvlNode * &k2){ AvlNode *k1=k2->left;//原树中,k2>k1,k1为k2的左孩子 k2->left=k1->right;//k1上移,k1的左子树变为k2的右子树 k1->right=k2; k2->height=max(height(k2->left),height(k2->right))+1; k1->height=max(height(k1->left),height(k1->right))+1; k2=k1;//这是旋转后的k2,也就变成了k1,其中k1的右子树为原先的k2 } |
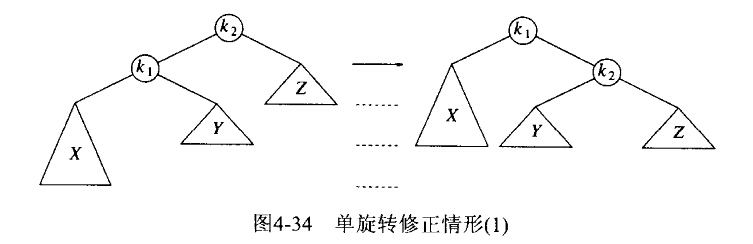
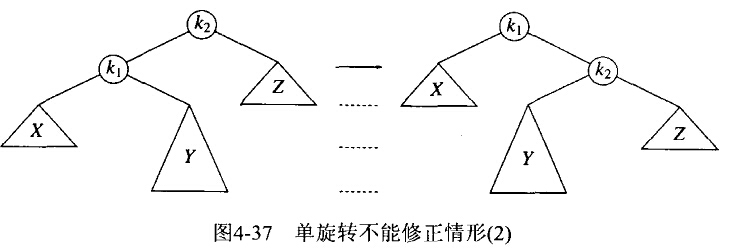
在原树中, ,于是在新树中
,于是在新树中 变成了
变成了 的右儿子,X和Z仍然分别是
的右儿子,X和Z仍然分别是 的左儿子和
的左儿子和 的右儿子。子树Y中包含
的右儿子。子树Y中包含 的那些结点,所以可以放在新树中
的那些结点,所以可以放在新树中 的左儿子的位置上。
的左儿子的位置上。
|
1 2 3 4 5 6 7 8 9 |
//右单旋转,RR类型 void AVLTree::rightChildSingleRotation(AvlNode * &k1){ AvlNode *k2=k1->right; k1->right=k2->left;//k1下移,k1的右子树变为k2的左子树 k2->left=k1; k1->height=max(height(k1->left),height(k1->right))+1; k2->height=max(height(k2->left),height(k2->right))+1; k1=k2; //这是旋转后的k1,也就变成了k2,其中k2的左子树为原先的k1 } |
让我们看一个例子,假设从初始的空AVL树开始插入项3、2和1,然后依序插入4到7。
在插入项目1时,AVL性质在根处被破坏。
插入4、5,插入5破坏了结点3处的AVL性质。注意,树的其余部分必须知晓该变化。如本例中,结点2的右儿子必须重新设置以链接到4而不是3。
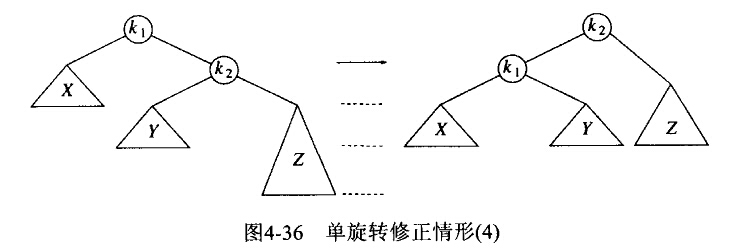
插入6,在根节点处产生了一个平衡问题,因为它的左子树高度是0而右子树高度为2。参见单旋转修正情况(4)。结点4的左子树变成了结点2的右子树。
插入7,它导致结点5处产生了平衡问题。
双旋转
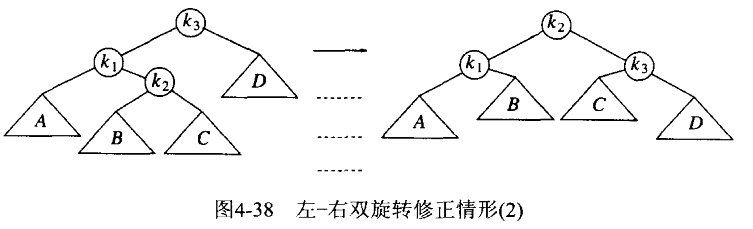
LR型双旋转——>两次单旋转,先逆(R),后顺(L)
|
1 2 3 4 5 6 7 8 9 10 11 12 |
void AVLTree::leftChildDoubleRotation(AvlNode * &k3){ AvlNode* k1=k3->left; AvlNode *k2=k1->right; k3->left=k2->right; k1->right=k2->left; k2->left=k1; k2->right=k3; k3->height=max(height(k3->left),height(k3->right))+1;//重新计算3个结点的高度 k2->height=max(height(k2->left),height(k2->right))+1;//重新计算3个结点的高度 k1->height=max(height(k1->left),height(k1->right))+1;//重新计算3个结点的高度 k3=k2; ////这是旋转后的k3,也就变成了k2,其中k2的右子树为原先的k3 } |
LR型双旋转——>两次单旋转,先对k3的左孩子做逆时针(RightChildSingleRotation),后顺(LeftChildSingleRotation)
|
1 2 3 4 |
void AVLTree::leftChildDoubleRotation(AvlNode * &k3){ rightChildSingleRotation(k3->left); leftChildSingleRoatation(k3); } |
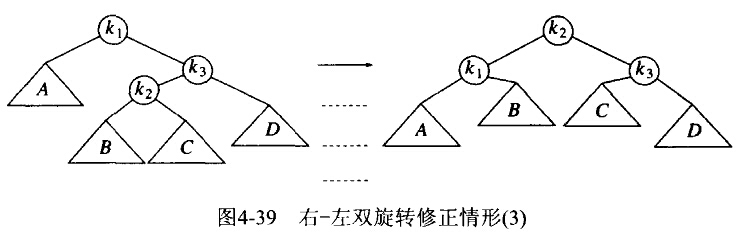
假设子树Y有一个根和两棵子树,所以可以把整棵树看成是四棵子树和3个结点连接。恰好树B或树C中有一棵比D深两层(除非它们都是空的)。如图,将 作为新的根,迫使
作为新的根,迫使 是
是 的左儿子,
的左儿子, 是
是 的右儿子。
的右儿子。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
//右--左双旋转 void AVLTree::rightChildDoubleRotation(AvlNode * &k1){ AvlNode* k3=k1->right; AvlNode *k2=k3->left; k1->right=k2->left; k3->left=k2->right; k2->right=k3; k2->left=k1; k3->height=max(height(k3->left),height(k3->right))+1;//重新计算3个结点的高度 k2->height=max(height(k2->left),height(k2->right))+1;//重新计算3个结点的高度 k1->height=max(height(k1->left),height(k1->right))+1;//重新计算3个结点的高度 k1=k2; //这是旋转后的k1,也就变成了k2,其中k2的左子树为原先的k1 } |
RL型双旋转——>两次单旋转,先对k1的右孩子做顺时针(LeftChildRotation),后逆时针(RightChildRotation)
|
1 2 3 4 |
void AVLTree::leftChildDoubleRotation(AvlNode * &k1){ leftChildSingleRotation(k1->right); rightChildSingleRoatation(k1); } |
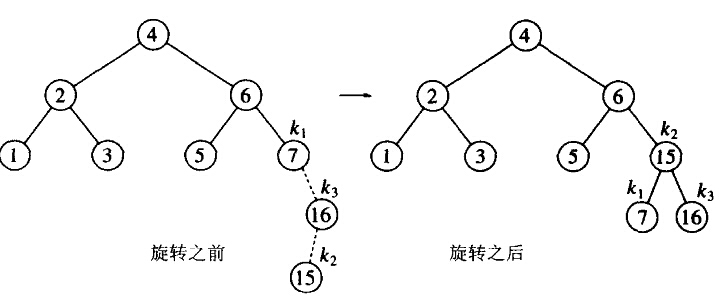
在前面例子的基础上倒序插入10-16,接着插入8,然后再插入9。插入15会引起结点7处的高度不平衡,需要通过一次右--左双旋转来解决。在不平衡的结点向下移动,以之为新的结点。
插入14,会引起结点7处的不平衡。修正该树的双旋转还是右--左双旋转。
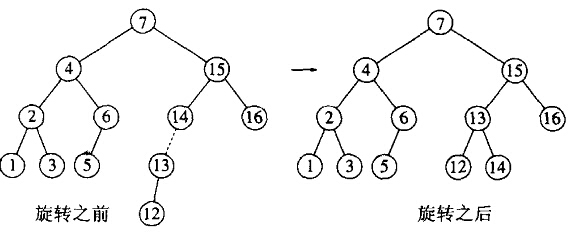
插入13,那么在根节点4处会引起不平衡。
12的插入也需要一个单旋转:(LL型)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
void AVLTree::AvlTree_Insert(const int &x,AvlNode * &t){ if(t==NULL){ t=new AvlNode(x,NULL,NULL); } else if(x< t->element){ AvlTree_Insert(x, t->left); if(height(t->left)-height(t->right)==2)//左子树比右子树高2 if(x<t->left->element)//LL类型 leftChildSingleRotation(t); else//LR类型 leftChildDoubleRotation(t); } else if(t->element<x){ AvlTree_Insert(x, t->right); if(height(t->right)-height(t->left)==2)//右子树比左子树高2 if(x>t->right->element)//RR类型 rightChildSingleRotation(t); else//RL类型 rightChildDoubleRotation(t); } else ;//同样的值,do nothing t->height=max(height(t->left),height(t->right))+1;//插入后的新高度 } |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
int _tmain(int argc, _TCHAR* argv[]){ AVLTree mytree; mytree.insert(3); mytree.insert(2); mytree.insert(1); mytree.insert(4); mytree.insert(5); mytree.insert(6); mytree.insert(7); mytree.insert(16); mytree.insert(15); mytree.insert(14); mytree.insert(13); mytree.insert(12); mytree.insert(11); mytree.insert(10); mytree.insert(8); mytree.insert(9); return 0; } |
Remove操作
对于一般的二叉查找树是怎样进行remove操作的。先根据二叉树的性质找到应该删除的结点t(如果有的话);如果t是个叶子结点,直接delete就好;如果它只有一颗非空的子树,那么就让这颗子树继承被删除结点的位子;而如果它有两颗非空的子树,就在右子树X中找到值最小的结点s,将s的data(值)写到t中,再在X中删除s(因为s的左子树一定为空,否则它就不是X中最小的了。另外,当然也可以在左子树中找值最大的结点。)

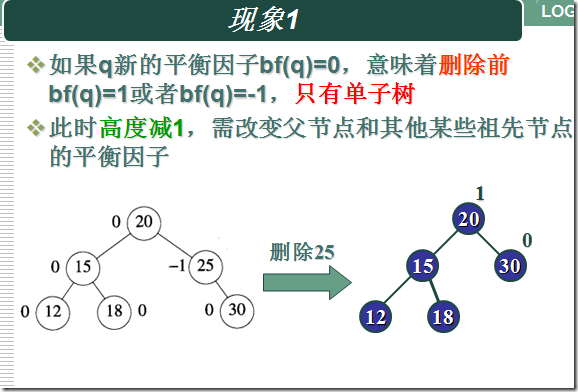
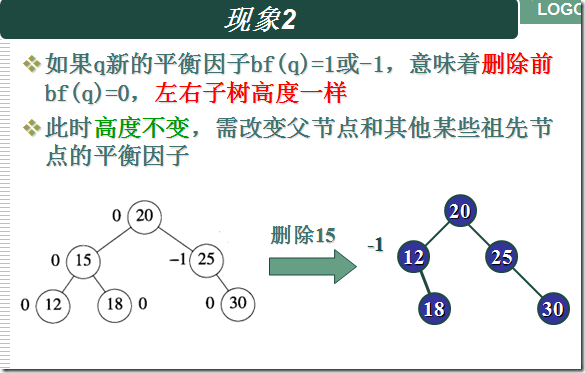
删除结点的操作依然需要分几种情况来分析:
1、假如要删除的结点是叶子结点:
那么直接删除这个结点,然后从它的父节点开始判断结点被删除以后是否依然满足平衡的特性,利用递归一直判断到根结点为止,利用递归很容易解决。
2、非叶子结点的删除:
非叶子结点的删除稍微麻烦,要分2种情况,这两种情况又各自有一个对称的情况。
假设第一个不满足平衡条件的结点为t,t的左子树为X,右子树为Y。
a) 以某结点t的左子树是删除结点操作之后最深的一个不满足平衡特性的结点,而它的左子树的深度大于右子树的深度。即(depth(l) - depth(r) == 2)
这说明是被删除的结点是T的左子树的右子树上。这是我们就利用右双旋转将其平衡。
b) 以某结点t的左子树是删除结点操作之后最深的一个不满足平衡特性的结点,而它的右子树的深度大于左子树的深度。即(depth(r) - depth(l) == 2)
被删除的结点是T的左子树的右子树上。这是我们就利用右单旋转将其平衡。
(1)在Y中删除了一个结点,而X的右子树不高于X的左子树。 LL
(2)在Y中删除了一个结点,而X的右子树高于X的左子树。 LR
(3)在X中删除了一个结点,而Y的左子树不高于Y的右子树。 RR
(4)在X中删除了一个结点,而Y的左子树高于Y的右子树。 RL
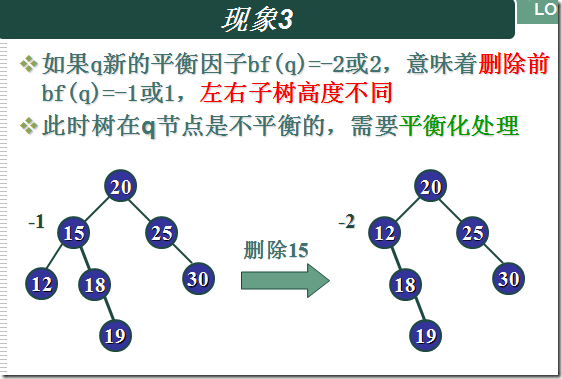
因为删除一个节点可能导致对其祖先结点的旋转,因此可以事先将要节点的祖先节点都保存下来。也就是从根结点到T1节点的路径。调整的时候是从T1的父节点开始往上(可能持续到根节点),因此其路径适合保存在栈中。这样可以依次从栈中弹出节点,判断是否需要调整。
需要注意的是,如果T1不是叶节点,需要查找其左子树的最右节点或者右子树的最左节点T2,这时的调整是从T2的父节点开始的,因此还需要记录T1到T2的路径,也就是说,最终得到的路径是从根结点到T2的。
调整某个节点的时候,记此节点为Tc,假设其父节点为Tp。需要将Tp的左(或者右)子树指针指向调整后得到的新Tc。
举一个例子:
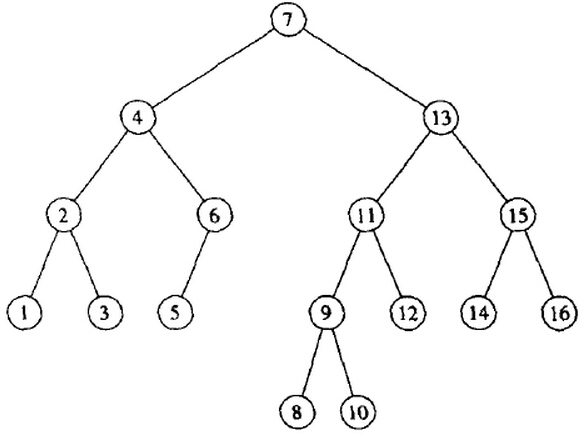
- 假设删除结点10,再删除结点12,这时候结点11就不满足平衡条件了,出现了LL的情形。
- 再假设先删除结点8,再删除结点12,这时候还是结点11不平衡,但这时类似情况LR。
- 再假设直接删除结点12,这时依然是结点11不平衡,这时虽然和情况LL,LR都不相同,但我们可以像图4-34那样经过一次单旋转使结点11变得平衡。(只不过这时图4-34中的Y和X一样高而不是比X矮1。)
- 这里特别需要注意的是,不管上上面3中情况中的哪一种情况,通过旋转使结点11平衡之后,它的高度都从2变成了1。这意味着,它的父亲的高度可能发生变化并且可能不再满足平衡。所以我们要从被删除点的父亲向上开始检查它的每个祖先,平衡每一个不满足平衡条件的祖先,直到找到了一个高度没有发生变化的祖先。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
void AVLTree::AvlTree_Remove(const int &x,AvlNode * &t){ if(!t)return; //在t的左子树X中删除一个结点 if(x<t->element){ AvlTree_Remove(x,t->left);//递归,压栈,从根结点到T1节点的路径。 if(height(t->right)-height(t->left)==2){ //右子树比左子树高2,那么在删除操作之前右子树比左子树高1, //也就是说t的右子树必然不为空,甚至必然有非空子树(高度至少为1)。 AvlNode *s=t->right; //Y的左子树高于Y的右子树. if(height(s->left)>height(s->right)) rightChildDoubleRotation(t);//右双旋转 //Y的左子树不高于Y的右子树. else rightChildSingleRotation(t);//右单旋转 } else t->height=max(height(t->left),height(t->right))+1; } else if(x>t->element){ AvlTree_Remove(x,t->right);//递归,压栈,从根结点到T1节点的路径。 if(height(t->left)-height(t->right)==2){ //右子树比左子树高2,那么在删除操作之前右子树比左子树高1, //也就是说t的右子树必然不为空,甚至必然有非空子树(高度至少为1)。 AvlNode *s=t->left; //X的右子树不高于X的左子树. if(height(s->right)>height(s->left)) leftChildDoubleRotation(t);//左双旋转 //X的右子树高于X的左子树. else leftChildSingleRotation(t);//左单旋转 } else t->height=max(height(t->left),height(t->right))+1; } else{ if(t->left&&t->right) //t的左右子树都非空,把remove操作转移到只有一个非空子树的结点或者叶子结点上去 { if (height(t->left)>height(t->right)) //把remove操作往更高的那棵子树上转移 { t->element=max_node(t->left)->element; AvlTree_Remove(t->element,t->left); } else{ //右子树中的最小值 t->element=min_node(t->right)->element; AvlTree_Remove(t->element,t->right); } } else{ AvlNode *oldnode=t; t=t->left?t->left:t->right; delete oldnode; } } } |
参考资料
1)http://www.cnblogs.com/Clingingboy/archive/2010/10/09/1846865.html
2)http://www.cnblogs.com/heqile/archive/2011/11/28/2265713.html