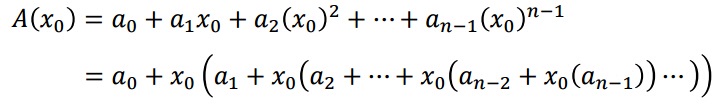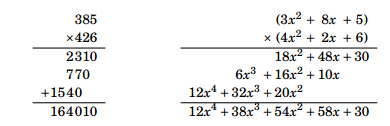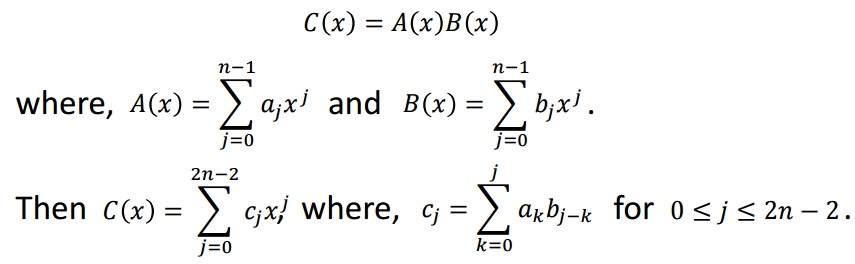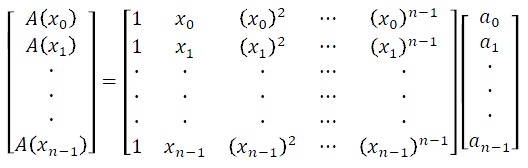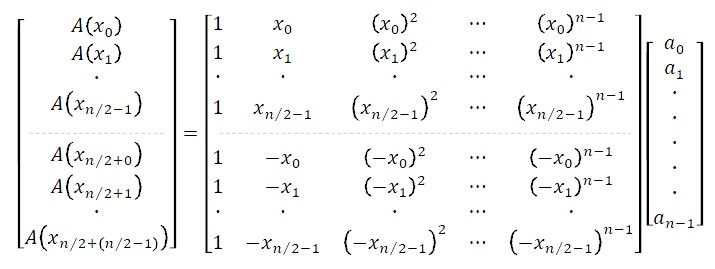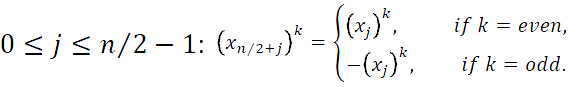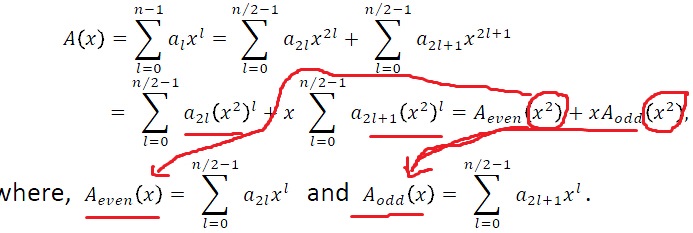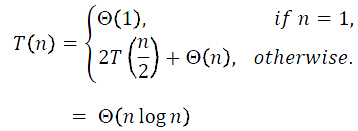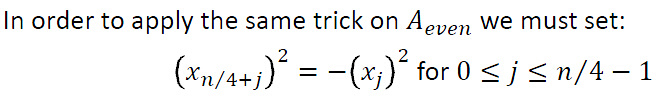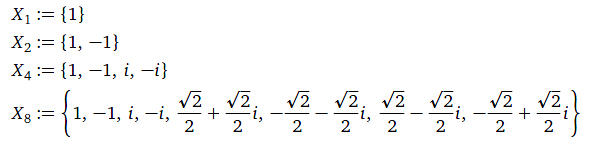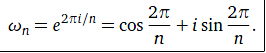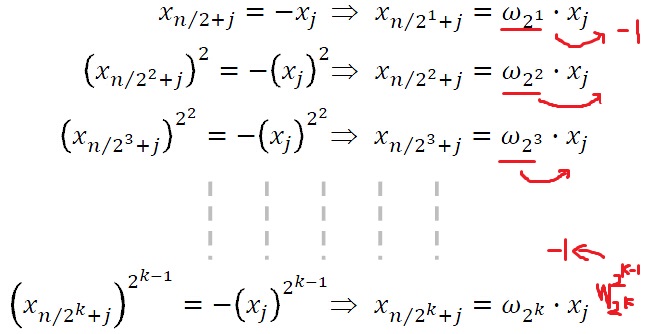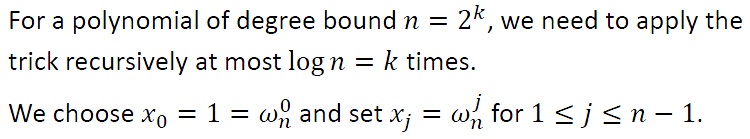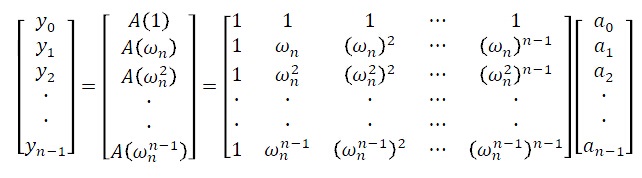FFT算法及其应用

多项式：一个以$x$为变量的多项式定义在一个代数域$F$上，将多项式函数$A(x)$表示为

$A(x)=\sum_{j=0}^{n-1}a_{j}x^{j}$

其中$a_{0},a_{1},...,a_{n-1}$为多项式系数。如果一个多项式$A(x)$的最高次的非零系数是$a_{k}$，则称$A(x)$的次数是k，$degree(A)=k$。任何一个大于一个多项式次数的整数都是该多项式的次数界。

1) 对于多项式加法：如果$A(x)$和$B(x)$是次数界为$n$的多项式，那么它们的和也是一个次数界为n的多项式$C(x)$。$C(x)=A(x)+B(x)$

$A(x)=\sum_{j=0}^{n-1}a_{j}x^{j}$

$B(x)=\sum_{j=0}^{n-1}b_{j}x^{j}$

$C(x)=\sum_{j=0}^{n-1}c_{j}x^{j}$

Horner Rule：对于多项式$A(x)$在给定点$x_{0}$的求值运算即计算$A(x_{0}$。在$\Theta(n)$时间复杂度内完成运算。

类似的，对于两个分别用系数向量$a_{0},a_{1},...,a_{n-1}$和$b_{0},b_{1},...,b_{n-1}$表示的多项式进行相加时，所需的时间为$\Theta(n)$。

2) 对于多项式乘法：举个例子

 $degree(C)=degree(A)+degree(B)$。

 注意观察，上式中$C(x)$的系数向量$\textbf{c}$其实是输入向量$\textbf{a}$和$\textbf{b}$。

点值表达(Point Value)：给定一组$n$个不同点集$\{x_{0},x_{1},...,x_{n-1}\}$，点值表达就是一个由n个点值对所组成的集合，$\{(x_{0},y_{0})\},\{(x_{1},y_{1})\},...,\{(x_{n-1},y_{n-1})\}$。

所有$x_{k}$不同，$\{(x_{0},A(x_{0}))\},\{(x_{1},A(x_{1}))\},...,\{(x_{n-1},A(x_{n-1}))\}$。

定理：（插值多项式的唯一性）对于任意n个点值对组成的集合$\{(x_{0},y_{0})\},\{(x_{1},y_{1})\},...,\{(x_{n-1},y_{n-1})\}$，所有$x_{k}$不同；那么存在唯一的次数界为$n$的多项式$A(x)$，满足$y_{k}=A(x_{k})?k=0,1,...,b-1$

其中范德蒙德矩阵表示为$V(x_{0},x_{1},...,x_{n-1})$，该矩阵的行列式值为$\prod_{0\leq j<k\leq n-1}(x_{k}-x_{j}$。如果所有$x_{k}$不同，则该矩阵是可逆的（非奇异）。给定点值表达，可以唯一确定系数$a_{j}$：

$\textbf{a}=V(x_{0},x_{1},...,x_{n-1})^{-1}y$

求解方法：

1. 利用LU分解可以在$O(n^{3}$的时间复杂度内求解；
2. 假定$n$为2的乘方，令（这是一个trick，但是很有用）

可以观察到

也就是说我们将原始的$n \times n$的矩阵划分成两个几乎相似的$\frac{n}{2}\times n$的矩阵。

观察到：

显然这是一个分治的思想，

我们这里用的技巧就是用$x$和$-x$来评估多项式A，但要注意，对于$A_{even}$和$A_{odd}$的输入都是$x^{2}$正数。

也就是说，

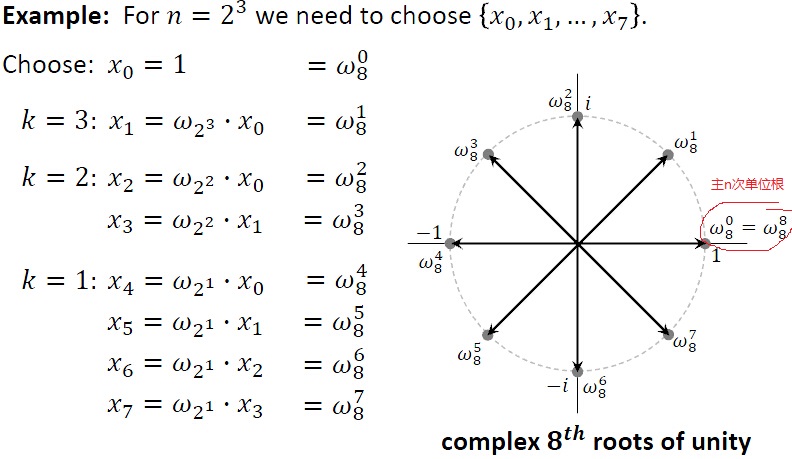
所以，可以针对上述做出规律总结：

单位复数根：$n$次单位复数根式满足$w^{n}=1$的复数$w$。对于$k=0,1,2,...,n-1$，这些根就是$e^{\frac{2\pi ik}{n}}$。值$w_{n}=e^{\frac{2\pi i}{n}}$称为主n次单位根。

n个n次单位复数根$w_{n}^{0},w_{n}^{1},...,w_{n}^{n-1}$在乘法意义下形成一个群。

$w_{n}^{0}=w_{n}^{n}=1$，$w_{n}^{j}w_{n}^{k}=w_{n}^{j+k}=w_{n}^{(j+k)mod n}$

用点值表达式求解多项式乘法。如果$C(x)=A(x)B(x)$，则对于任意点$C(x_{k})=A(x_{k})B(x_{k})$。由于C的次数界为$2n$，要插值获得唯一的多项式C，需要2n个点值对。必须对A和B的点值表达进行扩展，使每个多项式都包含$2n$个点值对。给定A的扩展点值表达$\{(x_{0},y_{0})\},\{(x_{1},y_{1})\},...,\{(x_{2n-1},y_{2n-1})\}$，B的对应扩展点值表达为$\{(x_{0},y_{0}^{'})\},\{(x_{1},y_{1}^{'})\},...,\{(x_{2n-1},y_{2n-1}^{'})\}$。

则C的点值表达为$\{(x_{0},y_{0}y_{0}^{'})\},\{(x_{1},y_{1}y_{1}^{'})\},...,\{(x_{2n-1},y_{2n-1}y_{2n-1}^{'})\}$。

应用：

1）数字乘法运算，和多项式乘法类似，A*B的操作就是用A每一位上的数字乘以B每一位上的数字。尤其是在大数乘法中，FFT可以大幅度加快运算。

2）给定A到B的不同长度路径详细数据，B到C的不同路径长度详细数据，求A到C不同长度路径的数量。可以把A到B和B到C不同长度的路径看成不同次数的项。例如：A到B有3条长度为4，2条长度为5的路径；B到C有1条长度为2，4条长度为3的路径。那么A到C不同长度路径的数量等于$(3*x^{4}+2*x^{5})*(4*x^{3}+1*x^{2})$得到的各项的系数，转化成多项式相乘问题之后，就可以利用FFT来加快运算速度了。

异曲同工：(30.1-6) 考虑两个集合A和B，每个集合包含取值范围在0~10n之间的n个整数。我们希望计算出A与B的笛卡尔和，定义如下：C={x+y:x∈A，y∈B}注意到，C中整数值的范围在0~20n之间。我们希望找到C中的元素，并且求出C中的每个元素可表示为A中元素与B中元素和的次数。请在O(nlgn)时间内解决问题。(提示：请用次数至多是$10n$的多项式来表示A和B)。

解法：多项式A与B是系数均为1的，指数为范围在$0~10n$之间的n个整数。计算$C(x)=A(x)*B(x)$可以用DFT在$O(nlgn)$时间内计算出。然后再遍历一下C，C的系数就是A与B的笛卡尔和项的出现次数。

3）在一个给定的数组中，判断是否有i,j,k满足a[i]+a[j]=a[k],有没有比较好的算法？

用fft可以做到nlogn求出所有可能的和，再用hashset存下来，然后遍历一遍看其中是否存在与原数组相同的数。但其实fft的复杂度和这些数的大小是相关的，这个nlogn就像01背包问题的dp解法一样，是个伪复杂度，并没有解决一般情况下的3sum问题。fft的复杂度严格来说是mlogm + n的，其中m是数组里每个数绝对值的最大值，n是数组大小。

实现：

对输入序列长度不是2的整数次幂，其实只要对长度取一下对数即可，例如：输入长度如果是37，首先把37*2，拓展成74（这个是FFT必须的），然后对74取log₂上取整即可，得到2⁷=128，因此在74后面再添加54个0。

参考资料：

1）CSE548-lecture-4.pdf

2）算法导论第30章

3）http://blog.csdn.net/z84616995z/article/details/24308087

4）https://en.wikipedia.org/wiki/3SUM#a.2Bb.3Dc

5）http://jeffe.cs.illinois.edu/teaching/algorithms/