Hash Table’╝łµĢŻÕłŚĶĪ©’╝ēÕ£©µÅÆÕģźŃĆüÕłĀķÖżŃĆüµÉ£Õ»╗ńŁēµōŹõĮ£õĖŖÕģʵ£ēŌĆ£ÕĖĖµĢ░Õ╣│ÕØ浌ČķŚ┤ŌĆØ ńÜäĶĪ©ńÄ░ŃĆéĶ┐Öń¦ŹĶĪ©ńÄ░õ╗źń╗¤Ķ«ĪõĖ║Õ¤║ńĪĆ’╝īõĖŹķ£ĆĶ”üõŠØĶĄ¢õ║ÄĶŠōÕģźÕģāń┤ĀńÜäķÜŵ£║µĆ¦ŃĆé
ÕÅ»µÅÉõŠøÕ»╣õ╗╗õĮĢµ£ēÕÉŹķĪ╣(named item)ńÜäÕŁśÕÅ¢µōŹõĮ£ÕÆīÕłĀķÖżµōŹõĮ£ŃĆéńö▒õ║ĵōŹõĮ£Õ»╣Ķ▒Īµś»µ£ēÕÉŹķĪ╣’╝īµēĆõ╗źhash tableÕÅ»õ╗źĶ¦åõĮ£õĖ║õĖĆń¦ŹÕŁŚÕģĖń╗ōµ×äŃĆéõĖĆĶł¼µāģÕåĄõĖŗ’╝īĶ«░ÕĮĢµś»ńö▒ĶŗźÕ╣▓ÕŁŚµ«Ąń╗䵳ÉńÜä’╝īµ»ÅõĖ¬ÕŁŚµ«ĄĶ┤¤Ķ┤Żõ┐ØÕŁśĶ«░ÕĮĢµēĆõ╗ŻĶĪ©Õ«×õĮōńÜäõĖƵ«Ąńē╣µ«Ŗń▒╗Õ×ŗńÜäõ┐Īµü»ŃĆéķö«(key’╝ēÕ░▒µś»ńö©µØźµ¤źµēŠńÜäµĢ░µŹ«µłÉÕæśŃĆéÕōłÕĖīĶĪ©’╝łHash table’╝īõ╣¤ÕŽµĢŻÕłŚĶĪ©’╝ē’╝īµś»µĀ╣µŹ«Õģ│ķö«ńĀüÕĆ╝(Key value)ĶĆīńø┤µÄźĶ┐øĶĪīĶ«┐ķŚ«ńÜäµĢ░µŹ«ń╗ōµ×äŃĆéõ╣¤Õ░▒µś»Ķ»┤’╝īÕ«āķĆÜĶ┐ćµŖŖÕģ│ķö«ńĀüÕĆ╝µśĀÕ░äÕł░ĶĪ©õĖŁõĖĆõĖ¬õĮŹńĮ«µØźĶ«┐ķŚ«Ķ«░ÕĮĢ’╝īõ╗źÕŖĀÕ┐½µ¤źµēŠńÜäķƤÕ║”ŃĆéĶ┐ÖõĖ¬µśĀÕ░äÕćĮµĢ░ÕŽÕüܵĢŻÕłŚÕćĮµĢ░’╝īÕŁśµöŠĶ«░ÕĮĢńÜäµĢ░ń╗äÕŽÕüܵĢŻÕłŚĶĪ©ŃĆé
õĖŠõŠŗµØźĶ»┤’╝īÕ”éµ×£µēƵ£ēÕģāń┤ĀķāĮµś»16bits’╝īõĖö õĖ║µŚĀń¼”ÕÅʵĢ┤µĢ░’╝īĶīāÕø┤õĖ║0~65535’╝īķ”¢ÕģłķģŹńĮ«õĖĆõĖ¬array A’╝īµŗźµ£ē65535õĖ¬Õģāń┤Ā’╝īń┤óÕ╝ĢÕÅĘńĀüõĖ║0~65535’╝īÕłØÕ¦ŗÕĆ╝Õģ©ķā©õĖ║0ŃĆéµ»ÅõĖĆõĖ¬Õģāń┤ĀÕĆ╝õ╗ŻĶĪ©ńøĖÕ║öÕģāń┤ĀńÜäÕć║ńÄ░µ¼ĪµĢ░’╝īµÅÆÕģźÕģāń┤Āi’╝īA[i]++’╝øÕłĀķÖżÕģāń┤Āi’╝īA[i]--ŃĆéµÉ£Õ»╗Õģāń┤Āi’╝īµŻĆµ¤źA[i]µś»ÕÉ”õĖ║0ŃĆéĶ┐Öń¦Źµ¢╣µ│ĢńÜäķóØÕż¢Ķ┤¤µŗģµś»arrayńÜäń®║ķŚ┤ÕÆīÕłØÕ¦ŗÕī¢µŚČķŚ┤ŃĆéĶ┐ÖÕģČÕ«×õ╣¤µś»ŌĆ£Ķ«ĪµĢ░µÄÆÕ║ÅńÜäµĆصā│ŌĆØŃĆé
Ķ┐ÖõĖ¬µ¢╣µ│ĢÕŁśÕ£©õĖżõĖ¬ķŚ«ķóś’╝ī1’╝ēÕ”éµ×£Õģāń┤Āµś»32-bits’╝īķéŻõ╣łarray AńÜäÕż¦Õ░ÅõĖ║2^{32}=4GB’╝īµśŠńäČarrayńÜäÕż¦Õ░ÅÕż¬Õż¦õ║åŃĆé2’╝ēÕ”éµ×£Õģāń┤Āµś»ÕŁŚń¼”õĖ▓ĶĆīķØ×µĢ┤µĢ░’╝īÕ░▒µŚĀµ│ĢĶó½µŗ┐µØźõĮ£õĖ║arrayńÜäń┤óÕ╝ĢŃĆé’╝łÕĮōńäȵ»ÅõĖ¬ÕŁŚń¼”ÕŁŚÕÅ»õ╗źńö©7-bitńÜäµĢ░ÕĆ╝’╝łÕŹ│ASCIIńĀüń╝¢ńĀü’╝ē’╝īõ║¦ńö¤ńÜäń┤óÕ╝ĢÕĆ╝õ╝ÜķØ×ÕĖĖÕż¦’╝ēŃĆé
µĢŻÕłŚĶĪ©ÕÅŖµĢŻÕłŚÕćĮµĢ░
µŖŖKeyķĆÜĶ┐ćõĖĆõĖ¬Õø║Õ«ÜńÜäń«Śµ│ĢÕćĮµĢ░µŚóµēĆĶ░ōńÜäÕōłÕĖīÕćĮµĢ░ĶĮ¼µŹóµłÉõĖĆõĖ¬µĢ┤Õ×ŗµĢ░ÕŁŚ’╝īńäČÕÉÄÕ░▒Õ░åĶ»źµĢ░ÕŁŚÕ»╣µĢ░ń╗äķĢ┐Õ║”Ķ┐øĶĪīÕÅ¢õĮÖ’╝īÕÅ¢õĮÖń╗ōµ×£Õ░▒ÕĮōõĮ£µĢ░ń╗äńÜäõĖŗµĀć’╝īÕ░åvalueÕŁśÕé©Õ£©õ╗źĶ»źµĢ░ÕŁŚõĖ║õĖŗµĀćńÜäµĢ░ń╗äń®║ķŚ┤ķćīŃĆé(Key mod Tablesize)ŃĆ鵜ŠńäČ’╝īÕŹĢÕģāńÜäµĢ░ńø«µś»µ£ēķÖÉńÜäŃĆéķ£ĆĶ”üÕ»╗µēŠõĖĆń¦ŹµĢŻÕłŚÕćĮµĢ░’╝īĶ»źÕćĮµĢ░Ķ”üÕ£©ÕŹĢÕģāõ╣ŗķŚ┤ÕØćÕīĆÕ£░ÕłåķģŹķö«ŃĆéńÉåµā│µāģÕåĄõĖŗÕ║öõ┐ØĶ»üõ╗╗õĮĢõĖżõĖ¬õĖŹÕÉīńÜäķö«µśĀÕ░äÕł░õĖŹÕÉīńÜäÕŹĢÕģāŃĆéÕĮōõĖżõĖ¬ķö«µĢŻÕłŚÕł░ÕÉīõĖĆõĖ¬ÕĆ╝µŚČ’╝īµłÉõĖ║Õå▓ń¬ü(collision)’╝łĶŗźĶĪ©ńÜäÕż¦Õ░ŵś»10ĶĆīķö«ńÜäõĖ¬õĮŹµś»ķøČ’╝ēŃĆé ÕźĮńÜäµ¢╣µ│Ģµś»õ┐ØĶ»üĶĪ©ńÜäÕż¦Õ░ŵś»ń┤ĀµĢ░’╝īÕÉīµŚČÕĮōĶŠōÕģźķö«õĖ║ķÜŵ£║µĢ┤µĢ░µŚČ’╝īµĢŻÕłŚÕćĮµĢ░õĖŹõ╗ģĶ┐Éń«Śń«ĆÕŹĢĶĆīõĖöķö«ńÜäÕłåķģŹÕŠłÕØćÕīĆŃĆé
µĢŻÕłŚµ│Ģ’╝łhashing’╝ēńÜäµĆصā│Õ░▒µś»µŖŖķö«ÕłåÕĖāÕ£©õĖĆõĖ¬ń¦░õĖ║µĢŻÕłŚĶĪ©(hash table)ńÜäõĖĆń╗┤µĢ░ń╗äõĖŁH[0,...,tablesize-1]’╝īÕŹ│µŖŖķö«µśĀÕ░äÕł░0~tablesize-1õĖŁńÜ䵤ÉõĖ¬µĢ░’╝īÕ╣ȵöŠÕł░ķĆéÕĮōńÜäÕŹĢÕģāŃĆé
- µŖŖķö«ķĆÜĶ┐ćhashÕćĮµĢ░ĶĮ¼µŹóµłÉõĖĆõĖ¬µĢ┤Õ×ŗµĢ░ÕŁŚ’╝īÕ░åĶ»źµĢ░ÕŁŚÕ»╣µĢ░ń╗äķĢ┐Õ║”ÕÅ¢õĮÖ’╝łkey mod tablesize)’╝īÕÅ¢õĮÖń╗ōµ×£õĖ║µĢ░ń╗äõĖŗµĀć’╝īÕ░åvalueÕŁśÕ£©õ╗źĶ»źµĢ░ÕŁŚõĖ║õĖŗµĀćńÜäµĢ░ń╗äń®║ķŚ┤õĖŁŃĆé
- ÕĮōõĮ┐ńö©ÕōłÕĖīĶĪ©Ķ┐øĶĪīµ¤źĶ»óńÜ䵌ČÕĆÖ’╝īÕŹ│ÕåŹµ¼ĪÕł®ńö©ÕōłÕĖīÕćĮµĢ░Õ░åkeyĶĮ¼µŹóõĖ║Õ»╣Õ║öńÜäµĢ░ń╗äõĖŗµĀć’╝īÕ╣ČÕ«ÜõĮŹÕł░Ķ»źń®║ķŚ┤ĶÄĘÕÅ¢valueŃĆé’╝łÕł®ńö©µĢ░ń╗äńÜäÕ«ÜõĮŹµĆ¦ĶāĮĶ┐øĶĪīµĢ░µŹ«Õ«ÜõĮŹ’╝ē
µśŠńäČ’╝īÕ”éµ×£µĢŻÕłŚĶĪ©ķĢ┐Õ║”mÕ░Åõ║Äķö«ńÜäµĢ░ķćÅn’╝īÕ░▒õ╝ÜÕÅæńö¤ńó░µÆ×’╝łcollision’╝ē’╝īÕ░▒õ╝ܵ£ēõĖżõĖ¬µł¢ĶĆģµø┤ÕżÜńÜäķö«Ķó½µĢŻÕłŚÕł░µĢŻÕłŚĶĪ©ńÜäÕÉīõĖĆõĖ¬ÕŹĢÕģāńÜäńÄ░Ķ▒ĪŃĆéÕŹ│õĮ┐mńøĖÕ»╣õ║ÄĶČ│Õż¤Õż¦’╝īĶ┐Öń¦Źńó░µÆ×Ķ┐śµś»õ╝ÜÕÅæńö¤ŃĆéÕ£©µ£ĆÕØÅńÜäµāģÕåĄõĖŗ’╝īµēƵ£ēńÜäķö«ķāĮõ╝ܵĢŻÕłŚÕł░µĢŻÕłŚĶĪ©ńÜäÕÉīõĖĆõĖ¬ÕŹĢÕģāµĀ╝õĖŁŃĆé
µĢŻÕłŚÕćĮµĢ░ńÜäķĆēµŗ®’╝ܵ»öÕ”éĶĪ©ńÜäÕż¦Õ░ŵś»10’╝īĶĆīķö«ńÜäõĖ¬õĮŹķāĮµś»0’╝īķéŻõ╣łÕÅ¢õĮÖńÜäµĢŻÕłŚÕćĮµĢ░Õ░▒õĖĆõĖ¬õĖŹÕźĮńÜäķĆēµŗ®ŃĆéÕźĮńÜäÕŖ×µ│Ģµś»õ┐ØĶ»üĶĪ©ńÜäÕż¦Õ░ŵś»ń┤ĀµĢ░ŃĆéÕĮōĶŠōÕģźńÜäķö«õĖ║ķÜŵ£║µĢ┤µĢ░µŚČ’╝īµĢŻÕłŚÕćĮµĢ░õĖŹõ╗ģń«ĆÕŹĢĶĆīõĖöķö«ÕłåķģŹÕØćÕīĆŃĆéķĆÜÕĖĖ’╝īķö«µś»ÕŁŚń¼”õĖ▓’╝īĶ┐Öń¦ŹµāģÕåĄõĖŗ’╝īµĢŻÕłŚÕćĮµĢ░ķ£ĆĶ”üõ╗öń╗åķĆēµŗ®ŃĆé
1’╝ēµŖŖÕŁŚń¼”õĖ▓õĖŁńÜäÕŁŚń¼”ńÜäASCIIńĀüÕĆ╝ńøĖÕŖĀĶĄĘµØźŃĆéĶ┐ÖµśŠńäȵś»õĖĆń¦ŹõĖŹÕØćÕīĆńÜäÕłåķģŹ’╝īÕøĀõĖ║µ▒鵩ĪÕÅ»ĶāĮõ╝ÜõĖŹĶĄĘõĮ£ńö©ŃĆé
|
1 2 3 4 5 6 7 |
int hashmap1(const string &key, int tablesize){ int hashVal = 0; for (int i = 0; i < key.length(); i++){ hashVal += key[i]; } return hashVal%tablesize; } |
2’╝ēÕüćĶ«ŠKeyĶć│Õ░æµ£ē3õĖ¬ÕŁŚń¼”ŃĆéµĢŻÕłŚÕćĮµĢ░ÕŬĶĆāÕ»¤ÕēŹ3õĖ¬ÕŁŚń¼”ŃĆé
|
1 2 3 |
int hashmap2(const string &key, int tablesize){ return (key[0] + 27 * key[1] + 729 * key[2]) % tablesize; } |
3’╝ēµČēÕÅŖķö«õĖŁńÜäµēƵ£ēÕŁŚń¼”ŃĆéÕģüĶ«Ėµ║óÕć║’╝īÕÅ»ĶāĮõ╝ÜÕ╝ĢĶ┐øĶ┤¤µĢ░’╝īÕ£©µ£½Õ░Šµ£ēķÖäÕŖĀńÜ䵥ŗĶ»ĢŃĆé
Horner ń«Śµ│Ģµś»õ╗źĶŗ▒ÕøĮµĢ░ÕŁ”Õ«Č William George Horner ÕæĮÕÉŹńÜäõĖĆń¦ŹÕżÜķĪ╣Õ╝ŵ▒éÕĆ╝ńÜäÕ┐½ķƤń«Śµ│Ģ’╝īÕ«×ķÖģõĖŖ’╝īĶ┐Öń¦ŹÕ┐½ķƤń«Śµ│ĢÕ£©õ╗¢õ╣ŗÕēŹÕ░▒ÕĘ▓ń╗ÅĶó½Paolo RuffiniõĮ┐ńö©Ķ┐ćõ║åŃĆéĶĆīõĖŁÕøĮµĢ░ÕŁ”Õ«Čń¦”õ╣Øķ¤ČµÅÉÕć║Ķ┐Öń¦Źń«Śµ│ĢĶ”üµ»öWilliam George Horner µŚ®600ÕżÜÕ╣┤ŃĆé
![]()
ńø┤µÄźĶ«Īń«ŚńÜäĶ»Ø’╝īķ£ĆĶ”üĶ┐øĶĪīńÜäõ╣śµ│Ģµ¼ĪµĢ░õĖ║’╝Ü ’╝ī
’╝ī
Hornerń╗ÖÕć║ńÜäń«Śµ│Ģ’╝Ü
![]()
µ×äķĆĀÕ║ÅÕłŚ:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
//ńö©Ķ«Īń«ŚµĢŻÕłŚÕćĮµĢ░ĶŖéń£üõĖŗµØźńÜ䵌ČķŚ┤µØźĶĪźÕü┐ńö▒µŁżõ║¦ńö¤ńÜäÕ»╣ÕØćÕīĆÕłåÕĖāńÜäÕćĮµĢ░ńÜäĶĮ╗ÕŠ«Õ╣▓µē░ int hashmap3(const string&key, int tablesize){ string s; if (key.size()>1024) //Õ”éµ×£strÕż¬ķĢ┐’╝īÕłÖÕŬÕÅ¢ÕēŹ1024õĖ¬ÕŁŚń¼” s = key.substr(0, 1024); else s = key; int hashVal = 0; for (int i = 0; i < key.length(); i++){ hashVal = 37 * hashVal + key[i]; //Horner µ│ĢÕłÖ } hashVal %= tablesize; if (hashVal < 0)//ÕģüĶ«Ėµ║óÕć║’╝īÕÅ»ĶāĮõ╝ÜÕ╝ĢĶ┐øĶ┤¤µĢ░’╝īķ£ĆĶ”üķÖäÕŖĀµĄŗĶ»Ģ hashVal += tablesize; return hashVal; } |
┬ĀĶ¦ŻÕå│ńó░µÆ×µ¢╣µ│Ģ
1ŃĆüÕłåń”╗ķōŠµÄźµ│Ģ
Õ░åµĢŻÕłŚÕł░ÕÉīõĖĆõĖ¬ÕĆ╝ÕŠŚµēƵ£ēÕģāń┤Āõ┐ØńĢÖÕł░õĖĆõĖ¬ķōŠĶĪ©õĖŁ’╝īÕÅ»õ╗źõĮ┐ńö©µĀćÕćåÕ║ōõĖŁĶĪ©ńÜäÕ«×ńÄ░µ¢╣µ│Ģ’╝łÕ”éµ×£ń®║ķŚ┤ń┤¦’╝īķü┐ÕģŹõĮ┐ńö©’╝īÕøĀõĖ║ÕģČÕ«×ńÄ░õĖ║ÕÅīÕÉæķōŠĶĪ©’╝ēµł¢ĶĆģķććńö©ÕģČõ╗¢ńÜäµĢ░µŹ«ń╗ōµ×ä’╝īÕ”éõ║īÕÅēµ¤źµēŠµĀæŃĆüńöÜĶć│µś»ÕÅ”Õż¢õĖĆõĖ¬µĢŻÕłŚĶĪ©’╝īÕ«āõ╗¼ńÜ䵤źµēŠķƤÕ║”ķāĮµ»öķōŠĶĪ©Ķ”üÕ┐½ŃĆéõĮåµś»µłæõ╗¼µ£¤µ£øńÜ䵜»µĢŻÕłŚÕćĮµĢ░ĶČ│Õż¤Õ£░ÕźĮŃĆüµ¦ĮĶČ│Õż¤Õ£░ÕżÜ’╝īµēĆõ╗źÕ»╣Õ║öńÜäķōŠĶĪ©ķāĮÕ║öĶ»źÕŠłń¤Ł’╝īõĖŹÕĆ╝ÕŠŚÕÄ╗Õ░ØĶ»Ģµø┤ÕżŹµØéńÜäń╗ōµ×äŃĆé
ÕĮōõĖĆõĖ¬HashTableÕż¬µ╗ĪÕÉÄ’╝īÕÅæńö¤Õå▓ń¬üńÜäµ”éńÄćÕ░▒õ╝ÜÕż¦Õż¦Õó×ÕŖĀŃĆ鵳æõ╗¼ńÜäńŁ¢ńĢźµś»’╝ÜÕĮōĶŠŠÕł░õ║ŗÕģłĶ«ŠÕ«ÜńÜäĶŻģĶĮĮÕøĀÕŁÉµŚČ’╝īÕ░▒µŖŖµ¦ĮõĮŹµē®Õ▒ĢµłÉÕĤÕģłńÜä2ÕĆŹõ╗źõĖŖ’╝łÕÅ¢µ£ĆÕ░ÅńÜäń┤ĀµĢ░’╝ē’╝īķ揵¢░Ķ┐øĶĪīÕåŹµĢŻÕłŚŃĆéÕĤÕģłńÜäHashTableÕ«īÕģ©ķćŖµöŠ’╝īńö│Ķ»Ęµ¢░ńÜäµø┤Õż¦ńÜäń®║ķŚ┤’╝īńäČÕÉĵŖŖÕĘ▓µ£ēńÜäÕģāń┤Āķ揵¢░µĢŻÕłŚÕł░µ¢░ńÜäHashTableŃĆéÕåŹµĢŻÕłŚÕ╝ĆķöĆÕŠłÕż¦’╝īõĮåµłæõ╗¼µ£¤µ£øńÜ䵜»ÕÅæńö¤ÕåŹµĢŻÕłŚńÜäµ¼ĪµĢ░ÕŠłÕ░æŃĆé
õŠŗÕŁÉ’╝ÜõĖĆõĖ¬ÕÅ»õ╗źÕŁśÕé©Õ£©õĖĆĶł¼µĢŻÕłŚĶĪ©õĖŁńÜäEmployeeń▒╗’╝īĶ»źń▒╗õĮ┐ńö©nameµłÉÕæśõĮ£õĖ║ķö«ÕĆ╝ŃĆé
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 |
#ifndef _HASHTABLE_H #define _HASHTABLE_H #include <string> #include <vector> #include <list> using namespace std; template<typename HashObj> class HashTable{ private: int capacity;//ÕĘ▓Õ«╣ń║│ńÜäÕģāń┤ĀõĖ¬µĢ░ int slots; //ÕÅ¢ń┤ĀµĢ░ double alpha; //loading factor vector<list<HashObj> > table;//the array of lists here two > has a space,>> is an operator int hashmap(const HashObj& key);//Õåģķā©µĢŻÕłŚÕćĮµĢ░’╝īĶ┤¤Ķ┤ŻÕ░åµĢ░µŹ«µśĀÕ░äÕł░[0’╝īslots-1] void rehash();//ÕĮōĶŠŠÕł░loading factorµŚČ’╝īµ¦ĮµĢ░µē®Õż¦õĖ║ÕĤµØźńÜä2ÕĆŹ’╝łÕÅ¢µ£ĆÕ░ÅńÜäń┤ĀµĢ░’╝ē’╝īĶ┐øĶĪīÕåŹµĢŻÕłŚ public: bool contain(const HashObj& key);//Õłżµ¢ŁõĖĆõĖ¬µĢ░µś»Õɔգ©HashTableõĖŁ bool insert(const HashObj& key); //µÅÆÕģźõĖĆõĖ¬Õģāń┤ĀÕł░HashTableõĖŁ //õ╗ÄHashTableõĖŁÕłĀķÖżõĖĆõĖ¬Õģāń┤ĀŃĆéÕ”éµ×£µīćÕ«ÜÕģāń┤ĀõĖŹÕ£©HashTableõĖŁ’╝īÕłÖÕłĀķÖżÕż▒Ķ┤ź’╝īĶ┐öÕø×false bool remove(const HashObj &key); HashTable(int slots = 10007, double alpha = 0.7) :slots(slots), alpha(alpha){ capacity = 0; table.resize(slots); } int getSlots(){ return slots; } void setSlots(int num){ slots = num; } }; //Õ░åstringĶĮ¼µŹóõĖ║int int hashString(const string&key){ string s; if (key.size() > 1024) //Õ”éµ×£strÕż¬ķĢ┐’╝īÕłÖÕŬÕÅ¢ÕēŹ1024õĖ¬ÕŁŚń¼” s = key.substr(0, 1024); else s = key; int hashVal = 0; for (int i = 0; i < key.length(); i++){ hashVal = 37 * hashVal + key[i]; //Horner µ│ĢÕłÖ } //hashVal %= tablesize; //if (hashVal < 0)//ÕģüĶ«Ėµ║óÕć║’╝īÕÅ»ĶāĮõ╝ÜÕ╝ĢĶ┐øĶ┤¤µĢ░’╝īķ£ĆĶ”üķÖäÕŖĀµĄŗĶ»Ģ // hashVal += tablesize; return hashVal; } class Employee{ private: string name; double salary; int seniority; public: Employee(string name = "", double salary = -1, int seniority = -1) :name(name), salary(salary), seniority(seniority){} bool operator ==(const Employee&item)const{ return this->name == item.name; } bool operator !=(const Employee&item)const{ return !(*this == item);// ķćŹĶĮĮĶ┐ćńÜä==ÕÅĘ } const string &getName()const{ return name; } int Employhash()const{ return hashString(name); } void setName(string str){ name = str; } void setSalary(double sala){ salary = sala; } void setSenirioty(int senior){ seniority = senior; } }; #endif |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 |
#include "HashTable.h" #include <assert.h> #include<cassert> #include<algorithm> //using namespace std; template<typename HashObj>int HashTable<HashObj>::hashmap(const HashObj& key){ int hashVal = key.Employhash(); hashVal %= slots; if (hashVal < 0)//ÕģüĶ«Ėµ║óÕć║’╝īÕÅ»ĶāĮõ╝ÜÕ╝ĢĶ┐øĶ┤¤µĢ░’╝īķ£ĆĶ”üķÖäÕŖĀµĄŗĶ»Ģ hashVal += slots; return hashVal; } //µŻĆµ¤źķōŠĶĪ©µś»ÕÉ”Ķ»źÕģāń┤ĀÕĘ▓ń╗ÅÕ£©ĶĪ©õĖŁõ║å’╝īÕ”éµ×£Ķ”üµÅÆÕģźķćŹÕżŹÕģā’╝ī //ķéŻõ╣łķĆÜÕĖĖńĢÖÕć║õĖĆõĖ¬ķóØÕż¢ńÜäµĢ░µŹ«µłÉÕæś’╝īÕĮōÕć║ńÄ░Õī╣ķģŹõ║ŗõ╗ȵŚČĶ┐ÖõĖ¬µĢ░µŹ«µłÉÕæśÕó×ÕŖĀ1. template<typename HashObj>bool HashTable<HashObj>::contain(const HashObj&key) { int index = hashmap(key); const list<HashObj> &whichlist = table[index]; return find(whichlist.begin(), whichlist.end(), key) != whichlist.end(); } //Õ”éµ×£ÕĘ«õĖ¬Õģāń┤Āµś»µ¢░ńÜäÕģāń┤Ā’╝īķéŻõ╣łõĖĆĶł¼Ķó½µÅÆÕł░ĶĪ©ńÜäÕēŹń½»’╝īÕøĀõĖ║µ£ĆÕÉĵÅÆÕģźńÜäÕģāń┤Āµ£Ćµ£ēÕÅ»ĶāĮõĖŹõ╣ģÕåŹµ¼ĪĶó½Ķ«┐ķŚ« template<typename HashObj> bool HashTable<HashObj>::insert(const HashObj &key) { int index = hashmap(key); list<HashObj> &whichlist = table[index]; if (find(whichlist.begin(), whichlist.end(), key) != whichlist.end()) return false; whichlist.push_back(key); capacity++; if (capacity*1.0 / slots > alpha) rehash(); return true; } template<typename HashObj> bool HashTable<HashObj>::remove(const HashObj &key) { int index = hashmap(key); list<HashObj> & whichlist = table[index]; typename list<HashObj>::iterator itr = find(whichlist.begin(), whichlist.end(), key); if (itr == whichlist.end()) return false; whichlist.erase(itr);//ÕłĀķÖżlistõĖŁõĖĆõĖ¬Õģāń┤Ā capacity--; return true; } template<typename HashObj>void HashTable<HashObj>::rehash(){ int oldSlots = getSlots(); int newSlots = oldSlots * 2; //while (!isPrime) vector<list<HashObj> > oldVector = table; for (int i= 0; i < table.size(); i++) table[i].clear(); table.resize(newSlots); //µłÉÕæśÕćĮµĢ░ÕÅ»õ╗źńø┤µÄźõĮ┐ńö©ń▒╗Õ«Üõ╣ēõĖŁńÜäõ╗╗õĖƵłÉÕæś(µĢ░µŹ«µłÉÕæśµł¢ÕćĮµĢ░µłÉÕæś) setSlots(newSlots); capacity = 0; for (int i = 0; i < oldVector.size(); i++){ typename list<HashObj>::iterator itr = oldVector[i].begin(); while (itr != oldVector[i].end()) insert(*(itr++)); } } |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
int _tmain(int argc, _TCHAR* argv[]){ const int arrsize = 9; HashTable<Employee> hashTable(7, 1.0);//ÕłÜÕ╝ĆÕ¦ŗĶ«Šµ¦ĮµĢ░õĖ║7 string names[arrsize] = { "hujintao", "jiangzeimng", "heizeming", "chaogai", "jingchengwu", "liangchaowei", "wenjiabao", "zhangsanbao", "zengxiaoxian" }; double salaries[arrsize] = { 111.1, 121.2, 132.2, 10.5, 19.8, 89.2, 99.2, 100.2, 10.2 }; Employee employee[arrsize]; for (int i = 0; i < arrsize; ++i){ employee[i].setName(names[i]); employee[i].setSalary(salaries[i]); employee[i].setSenirioty(i + 1); } for (int i = 0; i < arrsize; ++i){ bool insertsuccess=hashTable.insert(employee[i]); } assert(hashTable.getSlots() == 14); //µē®Õ«╣ÕÉĵ¦ĮµĢ░Õ║öĶ»źõĖ║17 for (int i = 0; i < arrsize; ++i){ assert(hashTable.contain(employee[i])); hashTable.remove(employee[i]); assert(!hashTable.contain(employee[i])); } return 0; } |
Õ£©Ķ┐Öķćī’╝īµŁżµŚČhashmapÕĆ╝õĖ║6’╝īµöŠÕģź(list) table[6]õĖŁ’╝īpush_backµś»Õ£©ķōŠÕ░ŠÕŖĀÕģź’╝ø
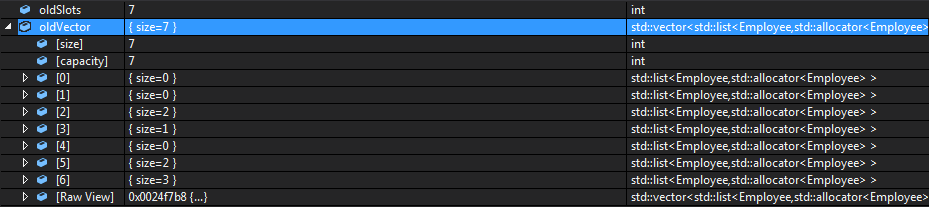


ÕĮōcapacityõĖ║8µŚČ’╝īķ£ĆĶ”ürehash()’╝īµ¦ĮõĮŹµĢ░Õ║öõĖ║ń┤ĀµĢ░’╝īĶ┐Öķćīń£üńĢźÕłżµ¢Ł’╝īńø┤µÄźµē®Õż¦õĖĆÕĆŹŃĆé(Ķ┐Öķćīµłæµ▓Īµ£ēĶ┐øĶĪīń┤ĀµĢ░µĄŗĶ»Ģ)

2ŃĆü õĖŹõĮ┐ńö©ķōŠĶĪ©ńÜäµĢŻÕłŚĶĪ©
Õłåń”╗ķōŠµÄźµĢŻÕłŚń«Śµ│ĢńÜäń╝║ńé╣µś»õĮ┐ńö©ķōŠĶĪ©’╝īńö▒õ║Äń╗Öµ¢░ÕŹĢÕģāÕłåķģŹÕ£░ÕØĆķ£ĆĶ”üµŚČķŚ┤’╝īÕ»╝Ķć┤ń«Śµ│ĢķƤÕ║”ĶŠāµģó’╝øõĮ┐ńö©ķōŠĶĪ©ńÜäÕÅ”õĖĆõĖ¬Ķ¦ŻÕå│Õå▓ń¬üµ¢╣µ│Ģµś»ÕĮōÕå▓ń¬üÕÅæńö¤µŚČÕ░ØĶ»ĢķĆēµŗ®ÕÅ”õĖĆõĖ¬ÕŹĢÕģā ’╝īńø┤Õł░µēŠÕł░ń®║ńÜäÕŹĢÕģāŃĆéÕ»╣õ║ÄõĖŹõĮ┐ńö©Õłåń”╗ķōŠµÄźµ│ĢńÜäµĢŻÕłŚĶĪ©µØźĶ»┤’╝īÕģČĶŻģÕĪ½ķōČÕŁÉÕ║öĶ»źõĮÄõ║Ä ’╝īń¦░õĖ║ŌĆ£µÄóµĄŗµĢŻÕłŚĶĪ©ŌĆØŃĆé
’╝īń¦░õĖ║ŌĆ£µÄóµĄŗµĢŻÕłŚĶĪ©ŌĆØŃĆé
2.1ŃĆüń║┐µĆ¦µÄóµĄŗ
Ķ┤¤Ķ┤Żń│╗µĢ░’╝łloading factor’╝ē
ÕüćĶ«ŠõĖĆõĖ¬µĢŻÕłŚĶĪ©ĶāĮÕ«╣ń║│nõĖ¬Õģāń┤Ā’╝īÕģʵ£ēmõĖ¬µ¦Į’╝łĶĪ©ķĢ┐’╝ē’╝īĶ┤¤ĶĮĮń│╗µĢ░õĖ║ n/mŃĆéÕüćÕ”éµĢŻÕłŚÕćĮµĢ░ĶāĮÕż¤õĮ┐ķö«ÕØćÕīĆÕłåķģŹ’╝īµ»ÅõĖĆõĖ¬Õģāń┤ĀµĢŻÕłŚÕł░mõĖ¬µ¦ĮõĮŹńÜäÕÅ»ĶāĮµĆ¦µś»ńøĖÕÉīńÜä’╝īÕ╣ČõĖÄÕģČõ╗¢Õģāń┤ĀÕĘ▓Ķó½µĢŻÕłŚÕł░õ╗Ćõ╣łõĮŹńĮ«ńŗ¼ń½ŗµŚĀÕģ│’╝łń¦░õĖ║ń«ĆÕŹĢõĖĆĶć┤µĢŻÕłŚ’╝īsimple uniform hashing’╝ēŃĆéÕ╣│ÕØćµāģÕåĄõĖŗµ¤źµēŠõĖĆõĖ¬Õģāń┤Āµś»Õɔգ©µĢŻÕłŚĶĪ©õĖŁńÜ䵌ČķŚ┤ÕżŹµØéÕ║”õĖ║ ŃĆé
ŃĆé
hash functionĶ«Īń«ŚÕć║µ¤ÉõĖ¬Õģāń┤ĀńÜäµÅÆÕģźõĮŹńĮ«’╝īĶŗźĶ»źõĮŹńĮ«õĖŖńÜäń®║ķŚ┤ÕĘ▓õĖŹÕåŹÕÅ»ńö©’╝īķéŻõ╣łÕŠ¬Õ║ÅÕŠĆõĖŗõĖĆõĖĆÕ»╗µēŠ’╝łÕ”éµ×£Õł░ĶŠŠÕ░Šń½»’╝īÕ░▒ń╗ĢÕł░Õż┤ķā©ń╗¦ń╗ŁÕ»╗µēŠ’╝ē’╝īÕŬĶ”üĶĪ©µĀ╝ĶČ│Õż¤Õż¦’╝īµĆ╗ÕÅ»õ╗źµēŠÕł░õĖĆõĖ¬ń®║ķŚ┤ŃĆéõĖżõĖ¬ÕüćĶ«Š’╝Ü1’╝ēĶĪ©µĀ╝(array)ĶČ│Õż¤Õż¦’╝ø2’╝ēµ»ÅõĖ¬Õģāń┤ĀķāĮÕż¤ńŗ¼ń½ŗ’╝łĶ┐ÖõĖ¬ÕüćĶ«ŠÕż¬Õż®ń£¤’╝ēŃĆéĶ¦éÕ»¤õĖŖÕøŠ’╝īÕ”éµ×£µ¢░Õģāń┤ĀõĖ║8’╝ī9’╝ī0’╝ī1’╝ī2’╝ī3õĖŁńÜäõ╗╗õĮĢõĖĆõĖ¬’╝īķāĮõ╝ÜĶÉĮÕ£©#3õĮŹńĮ«õĖŖŃĆé’╝łÕŹ│õĮ┐ĶĪ©ńøĖÕ»╣ĶŠāń®║’╝īÕŹĀµŹ«ńÜäÕŹĢÕģāõ╣¤õ╝ÜÕ╝ĆÕ¦ŗÕĮóµłÉõĖĆõ║øÕī║ÕØŚ’╝ēµ¢░Õģāń┤ĀÕ”éµ×£µś»4µł¢5µł¢6µł¢7’╝īµēŹõ╝ÜĶÉĮÕ£©ńøĖÕ║öńÜäõĮŹńĮ«õĖŖŃĆéõ╣¤Õ░▒µś»Ķ»┤’╝īÕ╣│ÕØćµÅÆÕģźµłÉµ£¼ńÜ䵳ÉķĢ┐Õ╣ģÕ║”Ķ┐£ķ½śõ║ÄĶ┤¤ĶĮĮń│╗µĢ░ńÜ䵳ÉķĢ┐Õ╣ģÕ║”ŃĆéĶ┐Öń¦ŹńÄ░Ķ▒Īń¦░õĖ║ŌĆ£õĖ╗ķøåÕøóŌĆØ(primary clustering)ŃĆéÕÅ»õ╗źĶ»üµśÄ’╝īõĮ┐ńö©ń║┐µĆ¦µÄóµĄŗńÜäķóäµ£¤µÄóµĄŗµ¼ĪµĢ░Õ»╣õ║ĵÅÆÕģźÕÆīõĖŹµłÉÕŖ¤ńÜ䵤źµēŠµØźĶ»┤Õż¦ń║”õĖ║ ’╝īĶĆīÕ»╣õ║ĵłÉÕŖ¤ńÜ䵤źµēŠµØźĶ»┤ÕłÖµś»
’╝īĶĆīÕ»╣õ║ĵłÉÕŖ¤ńÜ䵤źµēŠµØźĶ»┤ÕłÖµś»
2.2ŃĆüõ║īµ¼ĪµÄóµĄŗ(quadratic probing)
õ║īµ¼ĪµÄóµĄŗõĖ╗Ķ”üńö©õ║ÄĶ¦ŻÕå│õĖ╗ķøåÕøóķŚ«ķóśŃĆéÕ”éµ×£hash functionĶ«Īń«ŚÕć║µ¢░Õģāń┤ĀńÜäõĮŹńĮ«õĖ║H’╝īĶĆīĶ»źõĮŹńĮ«Õ«×ķÖģõĖŖÕĘ▓Ķó½õĮ┐ńö©’╝īķéŻõ╣łõŠØµ¼ĪÕ░ØĶ»Ģ ’╝īĶĆīõĖŹµś»ÕāÅń║┐µĆ¦µÄóµĄŗķ鯵ĀĘÕ░ØĶ»Ģ
’╝īĶĆīõĖŹµś»ÕāÅń║┐µĆ¦µÄóµĄŗķ鯵ĀĘÕ░ØĶ»Ģ ŃĆé
ŃĆé
Õ»╣õ║Äń║┐µĆ¦µÄóµĄŗµØźĶ»┤’╝īĶ«®µĢŻÕłŚĶĪ©Ķ┐æõ╣ÄÕĪ½µ╗ĪÕģāń┤ĀõĖŹµś»ÕźĮõĖ╗µäÅ’╝øÕ»╣õ║ÄÕ╣│µ¢╣µÄóµĄŗ’╝īµāģÕåĄ ńöÜĶć│µø┤ń│¤’╝ÜõĖƵŚ”ĶĪ©Ķó½ÕĪ½µ╗ĪĶČģĶ┐ćõĖĆÕŹŖ’╝īĶŗźĶĪ©ńÜäÕż¦Õ░ÅõĖŹµś»ń┤ĀµĢ░’╝īńöÜĶć│Õ£©ĶĪ©Ķó½ÕĪ½µ╗ĪõĖĆÕŹŖõ╣ŗÕēŹ’╝īÕ░▒õĖŹĶāĮõ┐ØĶ»üµēŠÕł░ń®║ńÜäÕŹĢÕģāõ║åŃĆé
Õ«ÜńÉå’╝ÜÕ”éµ×£ĶĪ©ńÜäÕż¦Õ░ÅõĖ║ń┤ĀµĢ░ ’╝īĶĆīõĖöµ░ĖĶ┐£õ┐صīüĶ┤¤ĶĮĮń│╗µĢ░Õ£©0.5õ╗źõĖŗ’╝łõ╣¤Õ░▒µś»Ķ»┤ĶČģĶ┐ć0.5Õ░▒ķ揵¢░ķģŹńĮ«Õ╣Čķ揵¢░µĢ┤ńÉåĶĪ©µĀ╝’╝ē’╝īķéŻõ╣łÕÅ»õ╗źõ┐ØĶ»üµ»ÅµÅÆÕģźõĖĆõĖ¬µ¢░Õģāń┤ĀńÜäµÄóµĄŗµ¼ĪµĢ░õĖŹÕżÜõ║Ä2ŃĆé
õĖŠõĖ¬õŠŗÕŁÉ’╝ÜTablesize=11’╝ī ’╝ī
’╝ī ’╝ī
’╝ī ’╝ī
’╝ī ’╝ī
’╝ī ’╝ī
’╝ī ’╝ī
’╝ī ’╝ī
’╝ī ’╝ī
’╝ī
Ķ»üµśÄ’╝Üõ╗żĶĪ©ńÜäÕż¦Õ░ÅTablesizeõĖ║õĖĆõĖ¬Õż¦õ║Ä3ńÜä’╝łÕźć’╝ēń┤ĀµĢ░ŃĆéÕÅ»Ķ»üÕēŹ õĖ¬ÕżćķĆēõĮŹńĮ«’╝łÕīģµŗ¼ÕłØÕ¦ŗõĮŹńĮ«
õĖ¬ÕżćķĆēõĮŹńĮ«’╝łÕīģµŗ¼ÕłØÕ¦ŗõĮŹńĮ« µś»õ║ÆÕ╝éńÜäŃĆéÕģČõĖŁõĖżõĖ¬õĮŹńĮ«µś»
µś»õ║ÆÕ╝éńÜäŃĆéÕģČõĖŁõĖżõĖ¬õĮŹńĮ«µś» ÕÆī┬Ā
ÕÆī┬Ā ’╝īÕģČõĖŁ
’╝īÕģČõĖŁ ŃĆéń¤øńøŠµ│Ģ’╝īÕüćĶ«ŠĶ┐ÖõĖżõĖ¬õĮŹńĮ«ńøĖÕÉī’╝īõĮå
ŃĆéń¤øńøŠµ│Ģ’╝īÕüćĶ«ŠĶ┐ÖõĖżõĖ¬õĮŹńĮ«ńøĖÕÉī’╝īõĮå ŃĆé
ŃĆé
ńö▒õ║ÄTablesizeõĖ║ń┤ĀµĢ░’╝īÕøĀµŁż’╝īµł¢ĶĆģ µł¢ĶĆģ
µł¢ĶĆģ ŃĆéń¼¼õĖĆń¦ŹµāģÕåĄµśŠńäČõĖŹÕÅ»ĶāĮ’╝īÕøĀõĖ║iŃĆüjõ║ÆÕ╝éŃĆéń¼¼õ║īń¦ŹµāģÕåĄ
ŃĆéń¼¼õĖĆń¦ŹµāģÕåĄµśŠńäČõĖŹÕÅ»ĶāĮ’╝īÕøĀõĖ║iŃĆüjõ║ÆÕ╝éŃĆéń¼¼õ║īń¦ŹµāģÕåĄ ’╝īõ╣¤õĖŹÕÅ»ĶāĮŃĆéõ╗ÄĶĆī’╝īÕēŹ
’╝īõ╣¤õĖŹÕÅ»ĶāĮŃĆéõ╗ÄĶĆī’╝īÕēŹ õĖ¬ÕżćķĆēõĮŹńĮ«µś»õ║ÆÕ╝éńÜäŃĆéÕ”éµ×£µ£ĆÕżÜµ£ē
õĖ¬ÕżćķĆēõĮŹńĮ«µś»õ║ÆÕ╝éńÜäŃĆéÕ”éµ×£µ£ĆÕżÜµ£ē õĖ¬õĮŹńĮ«Ķó½õĮ┐ńö©’╝īķéŻõ╣łń®║ÕŹĢÕģāµĆ╗ĶāĮÕż¤µēŠÕł░ŃĆéµ£ēõĖżńé╣ķ£ĆĶ”üĶ«░õĮÅ
õĖ¬õĮŹńĮ«Ķó½õĮ┐ńö©’╝īķéŻõ╣łń®║ÕŹĢÕģāµĆ╗ĶāĮÕż¤µēŠÕł░ŃĆéµ£ēõĖżńé╣ķ£ĆĶ”üĶ«░õĮÅ
- Õ”éµ×£Õō¬µĆĢĶĪ©µ£ēµ»öõĖĆÕŹŖÕżÜõĖĆõĖ¬ńÜäõĮŹńĮ«Ķó½ÕĪ½µ╗Ī’╝īķéŻõ╣łµÅÆÕģźķāĮµ£ēÕÅ»ĶāĮÕż▒Ķ┤ź’╝łĶÖĮńäČĶ┐Öń¦ŹÕÅ»ĶāĮµĆ¦µ×üÕ░Å’╝ē
- ĶĪ©ńÜäÕż¦Õ░ŵś»ń┤ĀµĢ░ŃĆéÕ”éµ×£õĖŹµś»ń┤ĀµĢ░’╝īķéŻõ╣łÕżćķĆēÕŹĢÕģāńÜäõĖ¬µĢ░ÕÅ»ĶāĮõ╝ÜķöÉÕćÅŃĆéõŠŗÕ”é’╝īĶŗźĶĪ©Õż¦Õ░ÅõĖ║16’╝īķéŻõ╣łÕżćķĆēÕŹĢÕģāÕŬĶāĮÕ£©ĶĘصĢŻÕłŚÕĆ╝1ŃĆü4µł¢9Ķ┐£ÕżäŃĆé
Õ£©µĢŻÕłŚĶĪ©õĖŁµĀćÕćåńÜäÕłĀķÖżµōŹõĮ£õĖŹĶāĮµē¦ĶĪī’╝īÕøĀõĖ║ńøĖÕ║öńÜäÕŹĢÕģāÕÅ»ĶāĮÕĘ▓ń╗ÅÕ╝ĢĶĄĘĶ┐ćÕå▓ń¬ü’╝īÕģāń┤Āń╗ĢĶ┐ćÕ«āÕŁśÕé©Õ£©Õł½ÕżäŃĆéõŠŗÕ”é’╝īÕłĀķÖż89’╝īķéŻõ╣łÕ«×ķÖģõĖŖµēƵ£ēÕē®õĖŗńÜäfindµōŹõĮ£ķāĮÕ░åÕż▒Ķ┤źŃĆé
Õ«×ńÄ░ÕżŹµØéÕ║”’╝Üõ║īµ¼ĪµÄóµĄŗķ£ĆĶ”üõĖĆõĖ¬ÕŖĀµ│Ģ ’╝īõĖĆõĖ¬õ╣śµ│Ģ’╝łĶ«Īń«Ś
’╝īõĖĆõĖ¬õ╣śµ│Ģ’╝łĶ«Īń«Ś ’╝ē’╝īÕÅ”õĖĆõĖ¬ÕŖĀµ│Ģ’╝īõ╗źÕÅŖModĶ┐Éń«ŚŃĆé
’╝ē’╝īÕÅ”õĖĆõĖ¬ÕŖĀµ│Ģ’╝īõ╗źÕÅŖModĶ┐Éń«ŚŃĆé
Ķ┐ÖõĖ¬Õģ¼Õ╝ÅĶĪ©µśÄõ║åÕÅ»õ╗źńö©ÕēŹķØóõĖĆõĖ¬HÕĆ╝µØźĶ«Īń«ŚõĖŗõĖĆõĖ¬HÕĆ╝’╝īĶĆīõĖŹķ£ĆĶ”üµē¦ĶĪīõ║īµ¼ĪµÄóµĄŗµēĆķ£ĆńÜäõ╣śµ│ĢŃĆé
õ║īµ¼ĪµÄóµĄŗÕÅ»õ╗źµČłķÖżõĖ╗ķøåÕøó’╝īõĮåÕÅ»ĶāĮõ╝ÜķĆĀµłÉµ¼ĪķøåÕøó(secondary clustering)ŃĆéõĖżõĖ¬Õģāń┤Āń╗Åhash functionĶ«Īń«ŚÕć║µØźńÜäõĮŹńĮ«ĶŗźńøĖÕÉī’╝īÕłÖµÅÆÕģźµŚČµēƵÄóµĄŗńÜäõĮŹńĮ«õ╣¤ńøĖÕÉīŃĆé
2.3ŃĆüÕÅīµĢŻÕłŚ
ÕÅīµĢŻÕłŚķĆēµŗ® ’╝īÕ░åń¼¼õ║īõĖ¬µĢŻÕłŚÕćĮµĢ░Õ║öńö©Õł░
’╝īÕ░åń¼¼õ║īõĖ¬µĢŻÕłŚÕćĮµĢ░Õ║öńö©Õł░ Õ╣ČÕ£©ĶĘØń”╗
Õ╣ČÕ£©ĶĘØń”╗ ’╝ī
’╝ī ’╝ī...ńŁēÕżäµÄóµĄŗŃĆé
’╝ī...ńŁēÕżäµÄóµĄŗŃĆé ńÜäķĆēµŗ®ķØ×ÕĖĖķćŹĶ”üŃĆé
ńÜäķĆēµŗ®ķØ×ÕĖĖķćŹĶ”üŃĆé
RõĖ║Õ░Åõ║ÄTablesizeńÜäń┤ĀµĢ░ŃĆé
Õ”éµ×£ÕÅīµĢŻÕłŚµŁŻńĪ«Õ«×ńÄ░’╝īķóäµ£¤µÄóµĄŗµ¼ĪµĢ░ÕćĀõ╣ÄÕÆīķÜŵ£║Õå▓ÕģźĶ¦ŻÕå│µ¢╣µ│ĢńÜäµāģÕĮóńøĖÕÉīŃĆéõĮåµś»Õ£©Õ«×ĶĘĄõĖŁ’╝īķö«õĖ║ÕŁŚń¼”õĖ▓µŚČ’╝īÕģȵĢŻÕłŚÕćĮµĢ░ńÜäĶ«Īń«ŚÕŠłĶĆŚµŚČŃĆé