Gradient Descent and Proximal Gradient Descent

考虑如下无约束凸优化问题 $min_{x\in R^{m}} \quad f(x)$

一个方法是使用Gradient Descent (GD)方法，也即使用以下的式子进行迭代求解：

对GD的一种解释是$x_{k}$沿着当前目标函数的下降方向走一小段，只要步子足够小，总能保证$f_{k+1}<=f_{k}$。

那么，我们就可以在点$x_{k}$附近把$f(x)$近似为

$\hat{f}(x, x_k) \doteq f(x_k) + \langle \nabla f(x_k), x - x_k \rangle + \frac{L}{2} ||x - x_k||^2$

把上面式子中各项重新排列下，可以得到：

$\hat{f}(x, x_k) \doteq f(x_k) + \langle \nabla f(x_k), x - x_k \rangle + \frac{L}{2} ||x - x_k||^2=\frac{L}{2} ||x - (x_k- \frac{1}{L}\nabla f(x_k)||^2+\varphi(x_{k})$

显然$\varphi(x_{k})$ dosen't depend on $x$.

显然$\hat{f}(x, x_k)$的最小值在$x_{k+1}=x_{k}- \frac{1}{L}\nabla f(x_k)$ 处获得。

所以从这个角度上看，GD的每次迭代是在最小化原目标的一个二次近似函数。

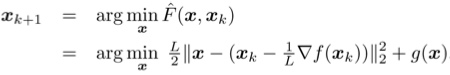
在很多最优化问题中,我们会加入非光滑的惩罚项g(x),比如常见的l1正则化项。但是可以借用二次近似的想法。这就是所谓的proximal gradient descent(PGD)算法。只要给定g(x)时下面的最小化问题能容易地求解，PGD就能高效地使用：

$prox_{\mu g}(z)=arg min_{x} \frac{1}{2}||x-z||_{2}^{2}+\mu g(x)$

比如$g(x)=||x||_{1}$时，能够通过soft thresholding获得：

$\text{prox}_{\mu g} (z) = \text{sign}(z) \max\{|z| - \mu, \ 0\}$

Part II：Gradient-descent technique: iterative hard-thresholding

考虑如下l_0稀疏求解问题：

（1）

或者    

值得注意的是：当eta < D^T D最大的特征值的导数时，算法会单调减小目标函数的值。在下文中会把iterative hard-thresholding解释为majorization-minimization algorithm(MM)。

显然优化目标的最小值在 处获得。这也正是算法四中迭代公式的由来。

对于（1）式给定k的大小，可以证明最后alpha的值就是每次迭代下列优化问题的解；

对于带有惩罚项的问题，最后alpha的值就是每次迭代下列优化问题的解

 

Part III：Proximal Gradient technique: iterative soft-thresholding

考虑如下l_1稀疏求解问题：

Proxmial Gradient和前者有些相似，\eta都是满足小于D^{T}D的最大特征值的倒数。

对于问题（5.8），给定参数\lamda的值，可以证明最后alpha的值就是每次迭代下列优化问题的解；

 

对于问题（5.10），最后alpha的值就是每次迭代下列优化问题的解；

 

 

参考资料:

1)http://www.cnblogs.com/breezedeus/p/3426757.html

2)Julien Mairal,Francis Bach,Jean Ponce,"Sparse Modeling for Image and Vision Processing"