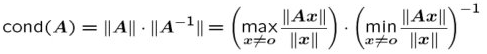共轭方向
无约束最优化方法的核心问题就是选择搜索方向
定义:设 为对称正定矩阵,若
为对称正定矩阵,若 中的两个方向
中的两个方向 和
和 满足
满足 ,则称这两个方向关于
,则称这两个方向关于 共轭,或称它们关于
共轭,或称它们关于 正交。
正交。
若 ,
, ,...,
,..., 为
为 中k个方向关于
中k个方向关于 共轭,满足
共轭,满足 ,也即
,也即 与
与 正交,称这组方向是A共轭的。
正交,称这组方向是A共轭的。
若A为单位阵,则这两个方向关于A共轭等价于两个方向正交。
二次函数  ,
, 为一个定点,
为一个定点,
 的等值面
的等值面 是以
是以 为中心的椭球面。
为中心的椭球面。
由于 ,A正定,所以
,A正定,所以 为
为 的极小点。
的极小点。
设 为等值面上一点,该等值面在点
为等值面上一点,该等值面在点 处的法向量
处的法向量 (注:二元函数一条等值线上一点的法向量即梯度)
(注:二元函数一条等值线上一点的法向量即梯度)
设 为等值面在
为等值面在 处的一个切向量,显然
处的一个切向量,显然 与
与 正交。同时,令
正交。同时,令 ,所以
,所以

结论:等值面上一点处的切向量与由这一点指向极小点的向量关于A共轭。
所以,极小化这个二次函数,若一次沿着  和
和 进行一维搜索,必将到达最小点。
进行一维搜索,必将到达最小点。
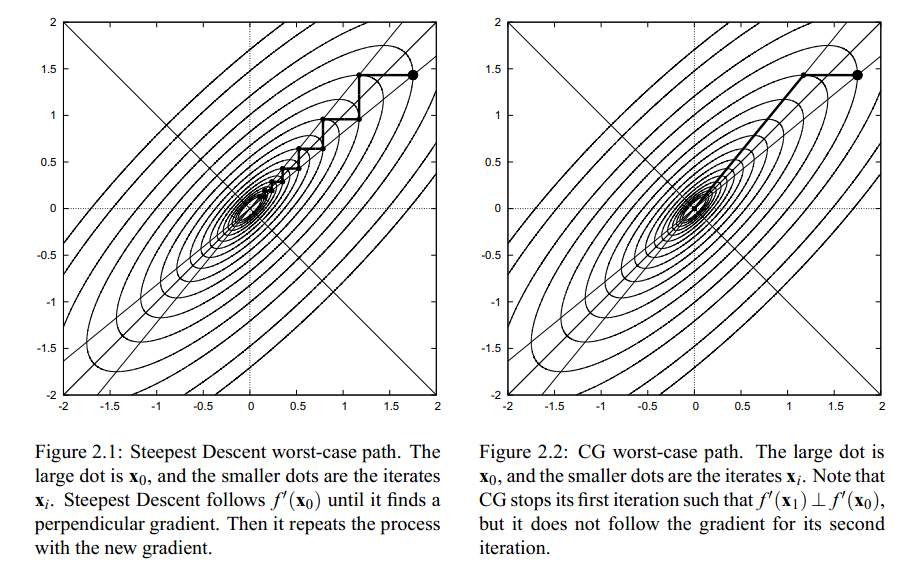
所谓最速真的是最速吗?
回顾最速下降法,用最速下降法极小化目标函数时,相邻两个搜索方向是正交的。
因为梯度是函数局部性质,从局部看,最速下降方向确实是函数值下降最快的方向,然而从整体看,由于锯齿现象的影响,则走过了许多弯路,使收敛速度大为减慢。最速下降法并不是收敛最快的方向。
对于二次型,从初始点 出发,最速下降法可由如下描述
出发,最速下降法可由如下描述
下图中极小点位于 ,令
,令 为每次迭代的误差向量,显然这个向量是无法计算的因为我们并不知道
为每次迭代的误差向量,显然这个向量是无法计算的因为我们并不知道 。
。
但是我们可以计算

记残差向量 ,可以发现
,可以发现 。
。
最速下降法即通过贪婪地减少误差项,在下一个点 时
时 (can only make square turns)。这个性质对于对称正定矩阵Hessian矩阵A的(二维)二次型来说,就意味着搜索方向一定会大于2次。为了确保迭代次数少于两次,就需要选择一个起始点
(can only make square turns)。这个性质对于对称正定矩阵Hessian矩阵A的(二维)二次型来说,就意味着搜索方向一定会大于2次。为了确保迭代次数少于两次,就需要选择一个起始点 ,
, 或者
或者 。当然我们无法计算误差向量。
。当然我们无法计算误差向量。
共轭梯度法的基本思想:利用已知点处的梯度构造一组共轭方向,并沿这组方向进行搜索,求出目标函数值得极小点。根据共轭方向的基本性质,这种方法具有二次终止性。
对于二次型的Hessian矩阵 为常值,所以可以构造一组搜索方向来避免redundant caculations。
为常值,所以可以构造一组搜索方向来避免redundant caculations。
假设有一组n个独立线性无关的方向向量 以及对应的尺度
以及对应的尺度

我们要做的就是将误差 迭代减小为0.假定我们知道
迭代减小为0.假定我们知道 并求解上式,则时间复杂度为
并求解上式,则时间复杂度为 。但是,如果方向向量
。但是,如果方向向量 是相互正交的,则可以在
是相互正交的,则可以在 求解得
求解得 。但是问题是我们是不知道
。但是问题是我们是不知道 的。
的。
又是先前的那个trick,我们计算

求解这个问题仍然是 ,相比
,相比 是相互正交的,我们让
是相互正交的,我们让 。求解
。求解 可通过左乘
可通过左乘 ,
,

那么我们可以求得

其中
共轭梯度法每一步迭代仅依赖于矩阵A和先前的迭代项,除了 ,实际上,
,实际上, 也可以写成先前的迭代项形式,因此我们只需要存储一些向量和矩阵A。
也可以写成先前的迭代项形式,因此我们只需要存储一些向量和矩阵A。
当A_{n\times n},CG方法可以在不超过n次迭代内得到精确解 。但是当在计算机上执行舍入运算时,这个性质无法保证。因为计算误差会减少方向向量之间的共轭性,从而使得算法可能会超过n次迭代。
。但是当在计算机上执行舍入运算时,这个性质无法保证。因为计算误差会减少方向向量之间的共轭性,从而使得算法可能会超过n次迭代。
CG的收敛率取决于
其中 为条件数,Hesse矩阵
为条件数,Hesse矩阵 的最小特征值
的最小特征值 ,最大特征值为
,最大特征值为 。CG终止条件为
。CG终止条件为 。这种最坏情况下CG的时间复杂度为
。这种最坏情况下CG的时间复杂度为 ,
, 为A中的非零迹项。显然,最坏情况发生在A的特征值为均匀分布,而较好的收敛率则出现在有多重特征值时。
为A中的非零迹项。显然,最坏情况发生在A的特征值为均匀分布,而较好的收敛率则出现在有多重特征值时。
所以,选择迭代终止条件也是一个很有讲究的问题。
用于二次函数的共轭梯度法
对于二次型

 为对称正定矩阵,
为对称正定矩阵, 和
和 为长度为
为长度为 的向量,
的向量, 为尺度。
为尺度。
假定 SPD,即
SPD,即
那么必有global minimum,最小点在point、line or plane上取得,不会有local minimum。
令 ,则
,则
算法步骤:
1)选取初始点 ,计算出目标函数在该点的梯度,若
,计算出目标函数在该点的梯度,若 ,则停止计算;否则,令第一个搜索方向
,则停止计算;否则,令第一个搜索方向 ,并记为此时方程的残差
,并记为此时方程的残差
2)沿方向 搜索,得到点
搜索,得到点 ,计算在点
,计算在点 处的梯度,若
处的梯度,若 ,则利用
,则利用 和
和 构造第2个搜索方向
构造第2个搜索方向 。先暂时假定我们已知该搜索方向。
。先暂时假定我们已知该搜索方向。
一般地,若已知点 和搜索方向
和搜索方向 ,则从
,则从 出发,沿
出发,沿 进行搜索,得到
进行搜索,得到

其中步长 满足
满足 。
。
令 ,求令
,求令 的极小点。
的极小点。
令 即
即
根据二次函数的梯度表达式,可得



所以根据上式可得

3)计算 在点
在点 处的梯度,若
处的梯度,若 ,则停止计算;否则,利用
,则停止计算;否则,利用 和
和 构造下一个搜索方向
构造下一个搜索方向 ,并使
,并使 和
和 关于
关于 共轭
共轭

上式两端左乘 ,并令
,并令

所以可得

综上分析,在第1个搜索方向取负梯度的前提下,伴随计算点的增加,构造出一组搜索方向,可以证明这组方向是关于A共轭的,因此,共轭梯度法具有二次终止性。(证明请参见《最优化方法》 陈宝林)
共轭梯度法:旨在求解线性方程Ax=b,A为正定矩阵。仅需一阶导数信息,但克服了最速下降法收敛慢的特点,又避免了牛顿法需要存储和计算Hessian矩阵并求逆的缺点。所以适合求解大型系统。当A is well-conditioned时,其远远快于其他方法如高斯消除法(时间复杂度 ,显然不适用于求解大型线性方程)。通过迭代方法去寻找
,显然不适用于求解大型线性方程)。通过迭代方法去寻找 的近似解。
的近似解。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
function x = conjgrad(A,b,tol) % CONJGRAD Conjugate Gradient Method. % X = CONJGRAD(A,B) attemps to solve the system of linear equations A*X=B % for X. The N-by-N coefficient matrix A must be symmetric and the right % hand side column vector B must have length N. % X = CONJGRAD(A,B,TOL) specifies the tolerance of the method. The % default is 1e-10. % By Yi Cao at Cranfield University, 18 December 2008 if nargin<3 tol=1e-10; end x = b; %initial point r = b - A*x; %residual if norm(r) < tol return end y = -r; %search direction z = A*y; s = y'*z; t = (r'*y)/s; %intial stepwidth x = x + t*y; %next point for k = 1:numel(b); r = r - t*z; if( norm(r) < tol ) return; end B = (r'*z)/s; %new search direction,composed of negative gradient direction and last search direction y = -r + B*y; z = A*y; s = y'*z; t = (r'*y)/s; x = x + t*y; end end |
Well-conditioned情况下:
|
1 2 3 4 5 6 7 8 9 |
n=1000; [U,S,V]=svd(randn(n)); s=diag(S); A=U*diag(s+max(s))*U'; % to make A symmetric, well-contioned b=randn(1000,1); tic,x=conjgrad(A,b);toc tic,x1=A\b;toc norm(x-x1) norm(x-A*b) |
|
1 2 3 4 5 6 7 8 9 |
实验结果:Elapsed time is 0.014805 seconds. Elapsed time is 0.029196 seconds. ans = 5.4321e-13 ans = 2.8499e+03 condition = 37.4486 |
Not Well-conditioned情况下:
|
1 2 3 4 5 6 7 8 9 10 |
clc,clear all n = 6000; m = 8000; A = randn(n,m); A = A * A'; b = randn(n,1); tic, x = conjgrad(A,b); toc norm(A*x-b) tic,x2=A\b;toc norm(A*x2-b) |
|
1 2 3 4 5 6 7 8 9 |
实验结果:Elapsed time is 7.117208 seconds. Elapsed time is 1.613006 seconds. ans = 3.0676e-09 ans = 1.4840e-12 condition = 2.7901e+04 |
参考资料:
1、陈宝林 《最优化理论与算法》 第二版
2、PaulKomarek “LogisticRegressionforDataMiningand High-DimensionalClassification”
3、http://blog.163.com/yuyang_tech/blog/static/216050083201210294100593/
矩阵条件数的性质:
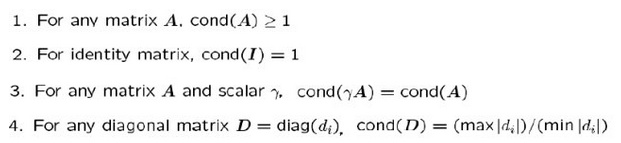
Matlab中计算矩阵条件数的函数:
|
1 2 3 4 5 |
cond(A)或cond(A, 2)用于计算2-条件数,它调用函数svd(A),适合于较小的矩阵。 cond(A, 1)计算1-条件数,它调用函数inv(A),运算量小于cond(A, 2)。 cond(A, inf)计算∞-条件数,它调用函数inv(A),等同于计算cond(A’, 1)。 condest(A)估算1-条件数,它使用lu(A)以及Higham和Tisseur 2000年提出的一个算法,特别适合于大型稀疏矩阵。 rcond(A)估算1-条件数的倒数,它使用lu(A)以及由LINPACK和LAPACK项目组开发的一个较老的算法。 |