图论二（二分图）

无权二分图（unweighted bipartite graph）

最大匹配（maximum matching）和完美匹配（perfect matching），以及用于求解匹配的匈牙利算法（Hungarian Algorithm）。

二分图：把一个图的顶点划分为两个不相交集 $U$ 和 $V$ ，并且图中每条边依附的两个顶点都分属于这两个互不相交的子集。准确地说：如果存在这样的划分，则此图为一个二分图。二分图的一个等价定义是：不含有「含奇数条边的环」的图。

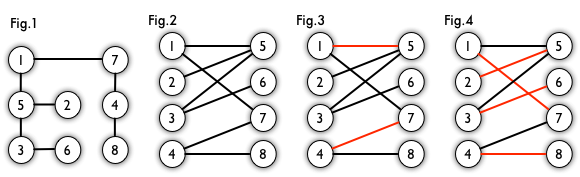
分析：如果这个无向图没有回路，那么它一定是可以二分的，我们直接就可以利用BFS来为二分图着色（根据当前节点的颜色，对其所有相邻节点涂另一个颜色）。如图1，我们可以将它转化成图2的形式。如果这个无向图有回路，如果回路的边数是偶数，那么它还是二分的，如果是奇数，那么它就不是二分的。如何判断回路的边数是奇数还是偶数呢？

结论：无向图 $G$ 为二分图的充分必要条件是， $G$ 至少有两个顶点，且其所有回路的长度均为偶数。

证明：1)必要性: 设 $G$ 为二分图 $<X,E,Y>$ 。由于 $X$ ， $Y$ 非空，故 $G$ 至少有两个顶点。若 $C$ 为 $G$ 中任一回路，令 $C = (v_{0},v_{1},v_{2},...,v_{l-1},v_{l}= v_{0})$ ，其中 $v_{i} (i = 0,1,...,l)$ 必定相间出现于 $X$ 及 $Y$ 中，不妨设 $(v_{0},v_{2},v_{4},...,v_{ l} = v_{0})\in X$ ， $(v_{1},v_{3},v_{5},...,v_{ l-1} )\in Y$ 。因此 $l$ 必为偶数，从而 $C$ 中有偶数条边。