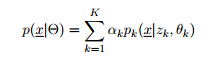Gaussian Mixture Model and EM (1)

Finite Mixture Model

给定数据集$D=\{x_{1},...x_{i},...,x_{N}\}$，$x_{i}\in R^{d}$。认为数据集由K个独立线性无关的分布$p_{k}$所产生，令$p(x)$表示为由这K个元素所组成的Mixture Model：

其中：

• $p_{k}(x|z_{k},\theta_{k})$为混合概率密度函数，$q\leq k \leq K$
• $z=(z_{1},...,z_{K})$是一个K维的二值化向量，其中只有一个元素为1，其他均为0。表示数据点x由第k个分布所产生。
• $\alpha_{k}=p(z_{k}=1)$是每个混合分布在整个分布中所占的比重，表示随机选取的数据点x由第k个分布所产生的概率，$\sum_{k=1}^{k}\alpha_{k}=1$。
• z是隐变量(Latent Varibale)。

对于由K个分布所组合的混合模型，其参数表示如下：

$\Theta=\{\alpha_{1},...,\alpha_{K},\theta_{1},...,\theta_{K}\}$

 Gaussian Mixture Model

每个 GMM 由 K 个 Gaussian 分布组成，每个 Gaussian 称为一个“Component”，这些 Component 线性加成在一起就组成了 GMM 的概率密度函数：

$p(x)=\sum_{k=1}^{K}\pi_{k}N(x|\mu_{k},\Sigma_{k})$

 $N(x|\mu_{k},\Sigma_{k}$是一个均值$mu_{k}$，协方差$Sigma_{k}$的高斯分布。

$p(z)=\prod_{k=1}^{K} \pi_{k}^{z_{k}}$;

随机选择一个数据点x，在给定隐变量z(向量)的情况下，表示x由第k个分布所产生，可以得出x的条件分布

$p(x|z_{k}=1)=N(x|\mu_{k},\Sigma_{k})$

$p(x|z)=\prod_{k=1}^{K} N(x|\mu_{k},\Sigma_{k})^{z_{k}}$

 所以x的边缘概率密度可由联合分布$p(z)p(x|z)$求和得到

$p(x)=\sum_{z}p(z)p(x|z)=\sum_{k=1}^{K}\pi_{k}N(x|\mu_{k},\Sigma_{k})$

 给定数据点$x$，计算由第$k$个 Component 生成的概率为$p(z_{k}=1|x)$记为$\gamma(x_{k})$。

$\gamma(x_{k})=p(z_{k}=1|x)=\frac{p(z_{k}=1)p(x|z_{k}=1)}{\sum_{j=1}^{K}p(z_{j}=1)p(x|z_{j}=1)}=\frac{\pi_{k}N(x|\mu_{k},\Sigma_{k})}{\sum_{j=1}^{K}\pi_{j}N(x|\mu_{j},\Sigma_{j})}$

 其中，$pi_{k}$视为$z_{k}=1$的先验概率，$\gamma(x_{k})$是为观察到x后$z_{k}$的后验概率。

最大似然（部分转载）

首先让我们看一个例子。 假设我们需要调查我们学校的男生和女生的身高分布。在校园中随便选取100个男生和100个女生。“男的左边，女的右边，其他的站中间！”。然后先统计抽样得到的100个男生的身高。

假设这100个男生身高独立同分布(高斯分布)，但是这个分布的均值u和方差∂²我们不知道，这两个参数就是我们要估计的。记作θ=[u, ∂]^T。那么其联合概率密度为

最大似然估计的思想：最合理的参数估计量应该使得从模型中抽取该n组样本观测值的概率最大，也就是概率分布函数或者说是似然函数最大。

通过抽取得到的那100个男生的身高和已知的其身高服从高斯分布，我们通过最大化其似然函数，就可以得到了对应高斯分布的参数θ=[u, ∂]^T了。那么，对于我们学校的女生的身高分布也可以用同样的方法得到了。

EM算法

如果没有“男的左边，女的右边，其他的站中间！”，那么你不知道抽取的那200个人里面的每一个人到底是从男生的那个身高分布里面抽取的，还是女生的那个身高分布抽取的。用数学的语言就是，抽取得到的每个样本都不知道是从哪个分布抽取的。(Mixture Model)

这个时候，对于每一个样本或者你抽取到的人，就有两个东西需要猜测或者估计的了，一是这个人是男的还是女的？二是男生和女生对应的身高的高斯分布的参数是多少？

每个样本的完整描述看做是三元组$\{x_{i},z_{i1},z_{i2}\}$，其中，$x_{i}$是第$i$个样本的观测值，也就是对应的这个样本的身高，是可以观测到的值。$z_{i1},z_{i2}$表示男生和女生这两个高斯分布中哪个被用来产生$x_{i}$，就是说这两个值标记这个样本到底是男生还是女生（的身高分布产生的）。确切的说，$z_{ij}$在$x_{i}$由第$j$个高斯分布产生时值为1，否则为0。例如一个样本的观测值为1.8，然后他来自男生的那个高斯分布，那么我们可以将这个样本表示为{1.8, 1, 0}。如果$z_{i1}$和$z_{i2}$的值已知，也就是说每个人我已经标记为男生或者女生了，那么我们就可以利用上面说的最大似然算法来估计他们各自高斯分布的参数。但是它们未知。

在 GMM 中，我们就需要确定 影响因子pi(k)、各类均值pMiu(k) 和 各类协方差pSigma(k) 这些参数

 EM算法思想：

 

 

 

 

 

 

 

 

 

 

 

 

OLS是普通最小二乘法，在满足相关假设的条件下，估计量是BLUE（最佳线性无偏估计）的；
ML是似然估计法，需要设定模型扰动项的分布，数据符合设定的分布时，统计量具有较好的性质；当正态分布时，ML估计与OLS估计相同；
GMM是广义矩估计法，要求数据满足设定的矩条件，比OLS、ML要求的假设少，适用范围较广；特殊条件下，GMM与OLS相同；
EM是期望最大化算法，严格说是一种优化算法，不能说是估计方法；在机制转换模型中应用较多；
Bayesian是贝叶斯估计法，采用先验信息和样本信息得到后验信息，进而进行参数估计和假设检验；OLS、ML、GMM均属于经典估计方法；
MCMC是马尔科夫链蒙特卡罗法，是贝叶斯估计中生成参数后验分布的方法。

 

 

参考资料：

1）http://home.deib.polimi.it/matteucc/Clustering/tutorial_html

2）GMM的EM算法实现   http://blog.csdn.net/abcjennifer/article/details/8198352

3）http://blog.csdn.net/zouxy09/article/details/8537620#comments