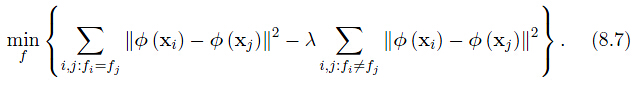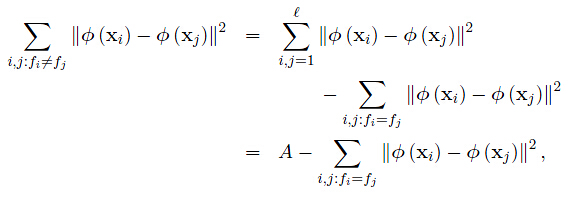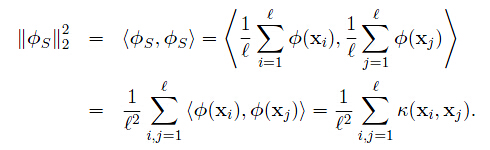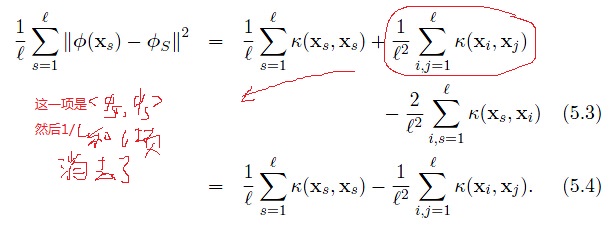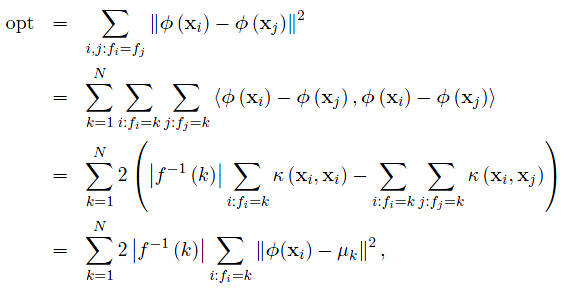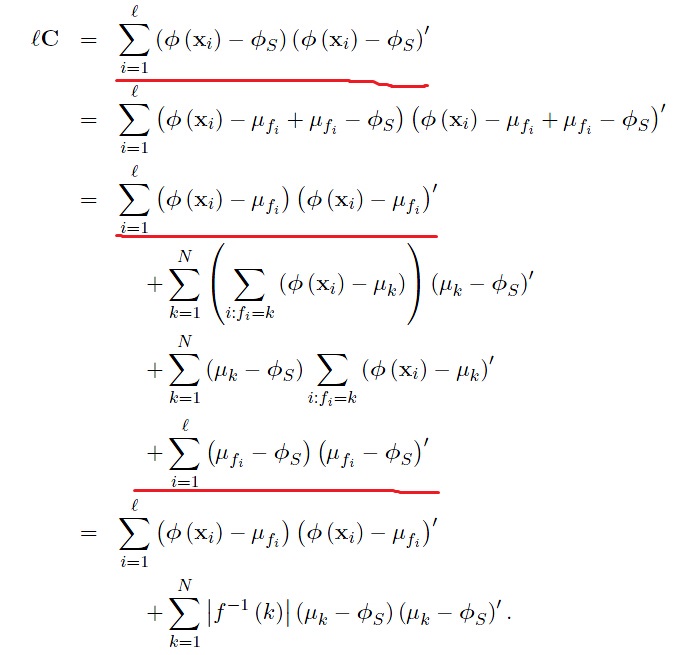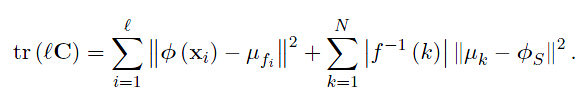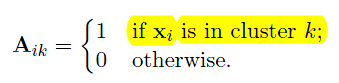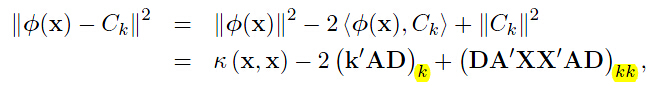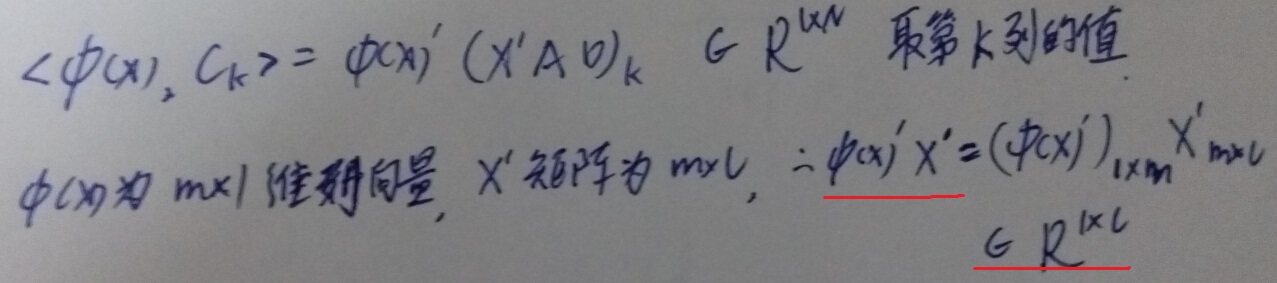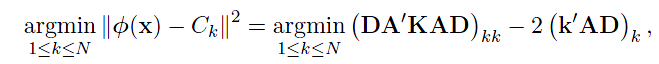rambo

聚类（四）从聚类本质看Kernel K-means

2015年9月11日 Machine Learning, 笔试面试 0 Comments

引出一个问题：一千万个高维数据，要进行k-means，要怎么操作？

  1. 用哈希表，把数据分成N块儿，再进行聚类。（怎么哈希才能保证你分的每一类中心点都比较合适）
  2. 先排序，再间隔得取几个点作为中心点，而海量数据的排序是可以用外部排序或哈希实现的。（高维数据，不方便排序）
  3. pca降维，（比如100万维的数据，降到1万维，还是没办法排序，而降到1维的话，丢失的信息太多了。）高维的话数据分布会很稀疏，这样基于距离度量数据相似性的算法会失效吗？

 一、从最本质的起点看聚类

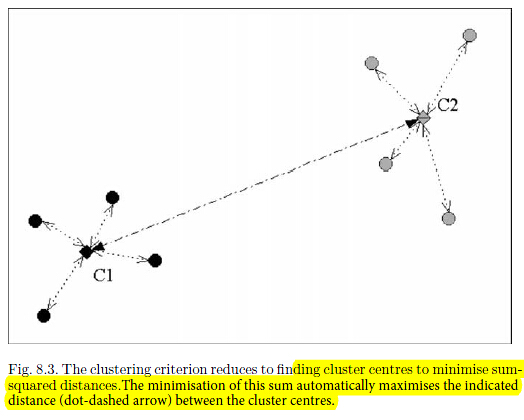
回顾K-means算法距离度量为每个数据点到其分配到的聚类中心的欧式平方距离。这样的划分方式会产生voronoi diagram（又叫泰森多边形或Dirichlet图，它是由一组由连接两邻点直线的垂直平分线组成的连续多边形组成。N个在平面上有区别的点，按照最邻近原则划分平面；每个点与它的最近邻区域相关联。）

主要思想是通过一个非线性映射，将输入空间中的数据点映射到高维特征空间中，并选取合适的核函数代替非线性映射的内积，在特征空间中进行聚类。
映射到高维空间：为了突出不同样本类别之间的特征差异，使得样本在核空间中变得线性可分（或近似线性可分）。

给定一组无标签的数据集S=\{x_{1},...,x_{l}\},x_{k}\in R^{N},k=1,2,...,l,被某种非线性映射\Phi映射到某一特征空间H，得到\Phi(x_{1}),...,\Phi(x_{l})，则输入空间的点积形式可以表示为\kappa(x_{i},x_{j})=<\Phi(x_{i}),\Phi(x_{j})>
所有样本可以组成一个核函数矩阵K_{i,j} =\kappa(x_{i},x_{j})

常用核函数：

  • 多项式核函数K(x,y)=(x\cdot y+1)^{d} ，d为整数，自定义参数
  • 高斯核函数 ，K(x,y)=(exp(-\beta \lVert x-y\rVert^{2}) ，\beta>0是自定义参数
  • 两层神经网络sigmod 核函数 K(x,y) =tanh(-b(x\cdot y)-c) ,其中b,c是自定义参数

QQ截图20150911221925

考虑目标函数最小化，下式包含了类间散度的分离性和类内散度的相似性，类内散度应该越相似，而类间散度应该应该越分散（会不会和LDA有点联系呢？嘿嘿！！）

QQ截图20150911163651

其中，f为映射函数，将样本映射到某一类。同时观察到，A对于给定的数据集为常数。

QQ截图20150911163826

所以，式8.7）可改写为

QQ截图20150911164444

补充公式：

QQ截图20150911203940

QQ截图20150911204022

QQ截图20150911205510

在训练集中X可能没有点经过\Phi映射后为\Phi_{S}。尽管我们不知道\Phi_{S}的具体信息，但是我们可以通过核的性质来计算其内积。所谓的Kernel Trick。

QQ截图20150911204132

QQ截图20150911205821

观察上式，每个点到其聚类中心的平方距离的平均值为核函数矩阵对角线上元素的平均值减去所有元素的平均值。

回到刚才的目标函数，等价于展开下式

QQ截图20150911203229

也就是说对于给定数目的聚类，最小化类内散度矩阵等同于最大化类间散度矩阵。最后一行可由式（5.4）推得。其中，QQ截图20150911211756为聚类k的中心。f(k)为映射到k类目的样本数。

这个中心点也常被认为是中值。所以上述准则也等价于下述准则：

QQ截图20150911211955

QQ截图20150911222041

算法流程：

QQ截图20150911232231

证明见“Kernel Methods for Pattern Analysis”第8章。上述定理指明了新数据点应该如何被分配到聚类中去。（千万不要认为这个是理所当然的，其实也是通过严格的证明得出的）

QQ截图20150911222752

缺点：同许多优化问题一样，这是非凸优化问题。（K-means采用贪婪迭代算法去寻找损失函数的局部最优，会因为非凸性而导致无法找到最优解；谱聚类则会对损失函数做条件放松，通过近似损失函数来进行全局最优）。

讨论：对于具有良好聚类性质的数据的核函数矩阵。自然的可以认为对于无关的两类应该具有零内积。

QQ截图20150911230642

考虑数据的协方差矩阵（数据做中心化(centering)），对其求导

QQ截图20150911231119

两边同取矩阵的迹，可得

QQ截图20150911232030

注意到右边第一项就是(8.19 process)中需要被聚类函数最小化的东西，而等式左边的值与聚类无关（也就是说是一个定值，有点厉害的！！！），所以上述式子等价于最大化下列目标函数（666666）

QQ截图20150911232719

1.1、贪婪算法：K-means

定理8.18证明我们可以通过寻求下述目标函数的最小化

QQ截图20150911233233

其中，聚类中心（means还是cetroids任意）C_{1},C_{2},....,C_{N} 为任意选取的初始化点。迭代更新分两个阶段，第一个阶段将数据点移动到离聚类中心最近的聚类中去，那么必然会减小(8.12)的值；第二阶段重新计算聚类中心，可以证明将聚类中心移动到一群数据点的中心会减小(8.12)的值。证明见“Kernel Methods for Pattern Analysis”第五章5.2

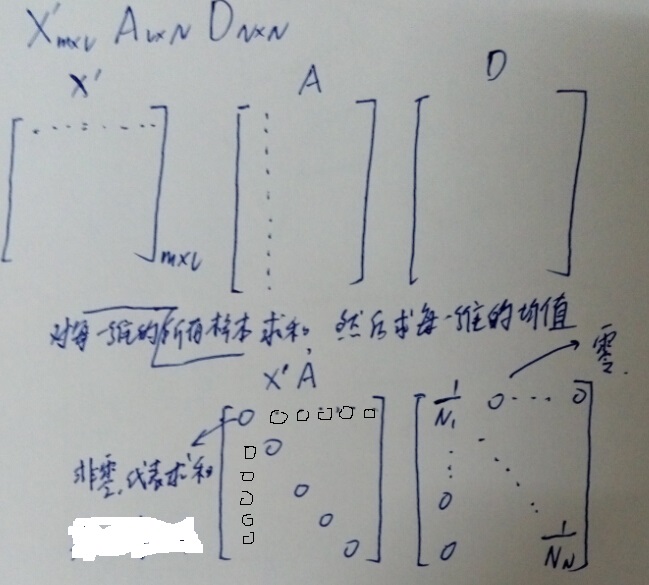
设计这样的矩阵A_{l\times N}，l个数据点，N个聚类

QQ截图20150911233958

其中，A的每一行只有一个元素为1，其他全为0（对于Soft K-means(Fuzzy)的话就是每一行之和为1）；而列之和则给出分配到各个聚类的数据点个数。

可以计算聚类中心C_{k}的坐标为矩阵X^{'}AD\in R^{m\times N}的列向量。

其中，X\in R{l\times m}是行向量为m维特征向量的数据点组成的数据矩阵，D\in R^{N\times N}的对角阵，对角线元素为A矩阵列向量之和的倒数，表示被分配该聚类的样本数的倒数。所以

QQ截图20150911235537

对于新的数据向量\phi(x)，与第k类聚类的聚类可以这样计算

QQ截图20150912000059

QQ截图20150912001155

同样的可以分析DA^{'}XX^{'}AD \in R^{N\times N}，下标kk就是取这个矩阵的对角线上的第k个值。

有了上面的分析，我们可以得出下述矩阵形式表达的聚类分配规则，\phi(x)按照下述规则分配给聚类k

QQ截图20150912001614

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
function [f,d] = dualkmeans(K,N)
% Performs dual K-means for ell samples specified by the kernel K
 
%
 
%INPUTS
 
% K = the kernel matrix
 
% N = the number of clusters desired
 
%
 
%OUTPUTS
 
% f = the cluster allocation vector
 
% d = the distances of the samples to their respective cluster centroids
 
 
% original kernel matrix stored in variable K
 
% clustering given by a ell x N binary matrix A
 
% and cluster allocation function f
 
% d gives the distances to cluster centroids
 
 
ell=size(K,1); %l为样本数，K为核函数矩阵
A = zeros(ell,N);% A为l*N矩阵
f = ceil(rand(ell,1)* N);
for i=1:ell
  A(i,f(i)) = 1;
end
change = 1;
while change == 1
  change = 0;
  E = A * diag(1./sum(A));  %diag(1./sum(A)就是D矩阵  E=AD，D的逆矩阵就是其本身
  Z = ones(ell,1)* diag(E'*K*E)'- 2*K*E; %agrmin (DA'KAD)_kk-2(K*AD)_k
  [d, ff] = min(Z, [], 2);
  for i=1:ell
   if f(i) ~= ff(i)
    A(i,ff(i)) = 1;
    A(i, f(i)) = 0;
    change = 1;
   end
  end
  f = ff;
end

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
clc,clear all;
load data;
K=x'*x; % use linear kernel
label=knkmeans(K,3);
spread(x,label)
 
function [label, energy] = knkmeans(K,init)
% Perform kernel k-means clustering.
%   K: kernel matrix
%   init: k (1 x 1) or label (1 x n, 1<=label(i)<=k)
% Reference: [1] Kernel Methods for Pattern Analysis
% by John Shawe-Taylor, Nello Cristianini
% Written by Michael Chen (sth4nth@gmail.com).
n = size(K,1);
if length(init) == 1
    label = ceil(init*rand(1,n));
elseif size(init,1) == 1 && size(init,2) == n
    label = init;
else
    error('ERROR: init is not valid.');
end
last = 0;
while any(label ~= last)
    [u,~,label] = unique(label);   % remove empty clusters
    label = label';
    k = length(u);
    E = sparse(label,1:n,1,k,n,n);
    E = bsxfun(@times,E,1./sum(E,2));
    T = E*K;
    Z = repmat(diag(T*E'),1,n)-2*T;
    last = label;
    [val, label] = min(Z,[],1);
end
[~,~,label] = unique(label);   % remove empty clusters
energy = sum(val)+trace(K);

RBF，最常用的径向基函数是高斯核函数，K(x,y)=(exp(\lVert x-y\rVert^{2})/(2\sigma^{2}) ，\sigma>0是自定义参数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
function K = rbf(coord,sig)
 
% Computes an rbf kernel matrix from the input coordinates
 
%INPUTS
 
% coord =  a matrix containing all samples as rows
 
% sig = sigma, the kernel width; squared distances are divided by
 
%       squared sig in the exponent
 
%
 
%OUTPUTS
 
% K = the rbf kernel matrix ( = exp(-1/(2*sigma^2)*(coord*coord')^2) )
 
 
%
 
%Author: Tijl De Bie, february 2003. Adapted: october 2004 (for speedup).
 
 
n=size(coord,1);
K=coord*coord'/sig^2;
d=diag(K);
K=K-ones(n,1)*d'/2;
K=K-d*ones(1,n)/2;
K=exp(K);

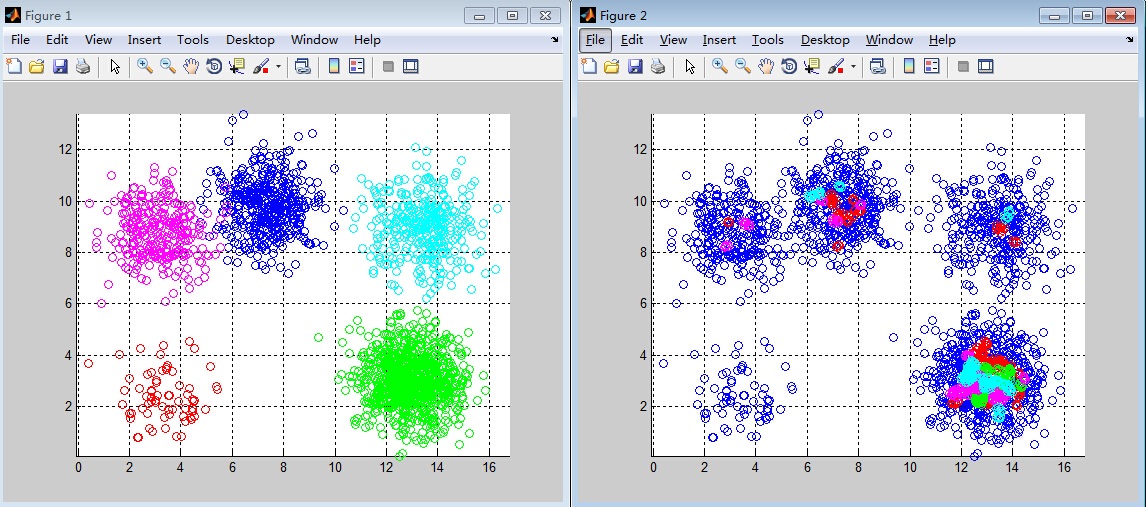
RBF核聚类效果图，左图为真实情形，右图为聚类效果。损失函数相比线性核大大减少，是前者的1/7。

QQ截图20150912005207

Kernel 有个问题嘞，核函数矩阵的计算有时候会超出内存。比如图像行乘列为36000时，matlab out of memory，该怎么解决这个问题呢？

 

参考资料：

1）http://blog.csdn.net/mpbchina/article/details/8018005

2）Taylor,"Kernel methods for pattern analysis"